例3

　物体と像を1m離して置くためには、物体とそれに対応する像の間のどこに＋4Dのレンズを正確に置かなければならないでしょうか？

答え：　XとX’は1m離れており、uは物体の距離でvは像の距離です。（下の図を見てください）。

絶対値での距離の測定（符号には関係なく）では、u＋v＝1mなので、v＝（1−u）mとなります。

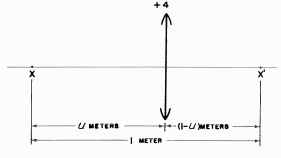
　レンズが物体と像の間にあるので、たとえどんな距離uが存在しようとも、物体の光の広がり（object vergence)Uはレンズ面ではマイナスでなくてはなりません。同様に推論すると、Vはプラスに違いありません。

だから、U＝とV＝となります。

ここで、私たちの一般式U＋P＝Vにこれらを代入します。

　　　　　　　　　　　　　　U＋P＝V

　　　　　　　　　　　　　

この方程式をuについて解くためには、私たちは分母を削除することによってそれを簡単にしなくてはなりません。この手作業は中学3年生の簡単な代数を必要とします。

　　　　　　　　　　　　 　−(1−u)＋4(u)(１−u)＝u

　　　　　　　　　　　　　　　　　　−1＋u＋4u−4u²＝u

　　　　　　　　　　　　　　　　　　　　−1＋4u−4u²＝0

　　　　−１を掛けると　　　　　　　　　　4u²−4u＋1＝0

　　　　　　　　　　　　　　　　　　　　　（2u−1）²＝0

　　　　平方根をとると　　　　　　　　　　　　　　2u−1＝0

　　　　　　　　　　　　　　　　　　　　　　　　　　　2u＝1

　　　　　　　　　　　　　　　　　　　　　　　　　　　　u＝　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　　1−u＝v＝

ゆえに、レンズは物体と像の両方から50cmのところに位置し、つまり、それらの真ん中になります。