例4

　左に置かれたプロジェクターからの収束光線が鮮明な、直径3cmの点状の像を右にあるスクリーン上に作ります。あなたは点の大きさを気にする必要はありませんが、プロジェクターを動かさずに右25cmのところに像を持っていきたいのです。あなたを助けるために役に立つ−2Dのレンズをあなたは持っています。あなたは像を置き換えるためにこのレンズをどこに持っていかなくてはなりませんか？

答え：　XからX’の距離は0.25mです。

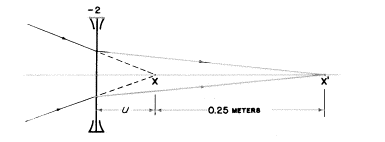
uを私たちのレンズから像X（それはもしレンズが最初に光線を横切っていなければプロジェクターによって産出されたものです！）までの距離としましょう。これは私たちの−2Dのレンズに対する物体の距離です。物体の光の広がり（object vergence)はU＝、P＝−2、像の光の広がり（image vergence)はV＝ですので、

　　　　　　　　　　　　 　　　　　　U＋P＝V

　　　　　　　　　　　 　　　　　　

　　 （0.25＋u）−2（u）（0.25＋u）＝u

　 0.25−0.5u−2u^２＝0

−１を掛けて　　　　　　　2u^２＋0.5u−0.25＝0

因数分解すると　　　 （2u−0.5）（u＋0.5）＝0

つまり、問題には２つの答えがあります。

　a) 　　2u＝0.5　

　　　　　 u＝0.25m　

　　　　　 u＝＋25cm

　b) 　　 u＝−0.5　

　　　　　 u＝−50cm

私たちはこれらの答えをどのように解釈すればいいのでしょうか？

a) −2レンズは元のスクリーンの前25cmに置かれないといけません。こうすると25cm離れた位置に投影された像を動かせます。

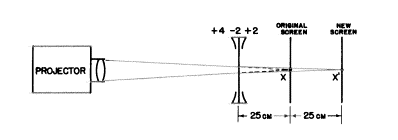
b) しかし、私たちは代数学的な解法から、もう1つの可能性を示唆されました（下図を見てください）。−50cmの物体距離uは、レンズに対し発散光線を送るようにレンズを置くことになります。これは私たちが映写機の像がXに作られたあとの光路にレンズを置いた時のみに可能です。この位置にスクリーンがない時光線は進み続けるでしょうが、その時それらは発散するでしょう。−50cmに置くと、−2Dのレンズは−2Dの光の広がり（vergence)を“見て”、−4Dの像の光の広がり（image vergence)を作ります。理由は、

　　　　　　　　　　　　 U＋P＝V

　　　　　　　　　　　−2＋(−2)＝−4

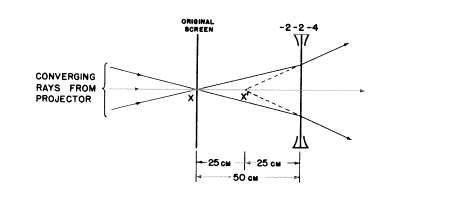
像の光の広がり（image vergence)−4は、私たちのレンズが25cm左に位置する虚像を作るということです。

本来の物点Xは最初の問題で述べた条件のように、確かに25cm右のX’に像を映しますが、もちろん私たちは数学的解法が最終的な虚像を含むことを先験的に知る方法がありませんでした。この答えが像の基準を満たしていようとも、付加した収束レンズなしにこの像を結ばせることは不可能ですから、この答えは実用的な解法ではなく、答え（a）が正しくて実用的なのです。