問題：

　物点Xは水のタンクの中に置かれ、タンクの端から40cmの距離にあり、タンクの端は半径5cmの凹面になっています。空気がタンクを包み込んでいます。

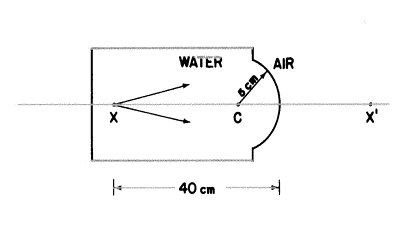
　a) どこに像点は結ばれるでしょうか？

　b) 屈折面の第1と第2焦点距離はどれだけでしょうか？

答え：

　a) U＋P＝V

U： 光線はXから曲面に突き当たるように発散していき、ゆえに、光の広がり（vergence)は面においてマイナスです。

　　物体空間の屈折率は水の屈折率であり、1.33です。ゆえに、物体の光の広がり（object vergence)である。

P： における屈折率の差はいつも像空間の屈折率から物体空間の屈折率を引いたものです:ここでは、（n_air−n_water）＝1.0−1.33＝−0.33です。r＝5cm＝（0.05m）ですが、ただ左から右へ入射してくる光に対して凹面ですので、マイナスになります。r＝−0.05mです。

　　だから、となります。

　　（ゆえに、像空間の屈折率が物体空間の屈折率より小さい時、私たちは凹面はプラスの屈折力を持つことが分かります。）

　V： 像光線の光の広がり（vergence)＝であり、n’はここでは像空間の屈折率であり空気ですからn’＝1.0となり、V＝です。

　それでは、Vに関する方程式を解くと：

　　　　U＋P＝V

　　　　

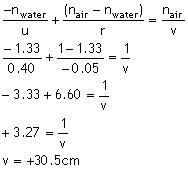
　Xの鮮明な像がX’、屈折面（水タンク側面）の右側30.5cmのところにできるでしょう。

　b) 第1焦点距離＝

　　　　　　　　f＝＋20cm（水の中）

　　 第2焦点距離＝

　　　　　　　　f’＝15.1cm（空気の中）

（両方は球面の軸上頂点から測られます。）