問題：

　a) 曲率半径が20cmの凸面鏡から50cmの距離に置かれた物体の像はどこにできるでしょうか？

　b) もし物体が5cmの高さであれば、それに対する像の大きさはどれだけになりますか？

　c) 必要とされる光学図を書きなさい。

答え：

　a)　 　 u＝−50cm、U＝−2D

　　　　　 P＝　このrは凸面鏡のものですから、rはプラスです。

　　　　　 P＝＝−10D

　　　 U＋P＝V

　　　−2−10＝−12D

　　　v＝＝−8.3cm

像は鏡の後ろ8.3cmのところに位置し、虚像です。これは鏡を見ている観察者にとっては像は鏡の後ろ8.3cmのところに位置しているかのように見えることを意味するのを思い出してください。

　b) 物体の大きさと比較した像の大きさは倍率（M）と呼ばれ、鏡から像と物体のそれぞれの距離と比例します。（ちょうど薄いレンズと同じように）

　　　　

像の大きさ＝×（物体の大きさ）＝×5cm＝＋0.83cm

ゆえに像の大きさは＋0.83cmとなり、前に述べた拡大の慣例でいうとMがプラスの時（ここのように）は像は正立になります。

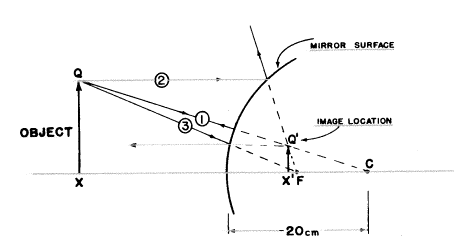
　c) 図：

　Qから発せられる光線の全てから既知の3本を選んでみます。

1. 光線1は面の曲率中心であるCに向かってまっすぐ進みます。この光線は“法線に沿って”いるので、この線に沿って正確に跳ね返されるでしょう。この反射された光線は（屈折の場合の）節点を通り“偏位しない”光線と等しくなります。（薄いレンズでは、節点は軸上の頂点にあるように見えました。しかし、単一曲面では節点はここのようにたまたまその面の曲率中心になります！）

2. 入射光線2は軸に平行に進み、F’を通って反射されなければなりません。

　これらの2本の光線はもちろん鏡を通り抜けることはできません。それらは鏡で反射されますが、鏡面の後ろのQ’から出ているように見え、そこは光線1と2の延長線が交わるところなのです。

　これらの2本の光線は私たちが必要な全てですが、もう1本の“既知の”光線があります。

3. 光線3はF（鏡ではF’と同じ位置にあります）の方へ進みます。それは軸に平行に反射されるでしょう。面を“通って”反対方向に延長すると、それはQ’から出ているようにも見えるでしょう。