第２節 角倍率(Angular Magnification)
角度は目に像がどれくらいの大きさで見えるかに関係があります。固定された同じ大きさの物体や像はあなたが近付けば大きく見え、遠ざかれば小さく見えるでしょう。あなたの網膜上の像は物体が近くに来ると角度で拡大されるのです（つまり、それは目の節点を頂点としたより大きな角を作ります）。しかし、それは他の角度―その同じ物体によって固定した参照距離で与えられたもの―を参照して角度で拡大されただけです。たとえば任意の参照距離（20フィートとします）に置かれた物体が網膜上に5°で向き合うと仮定します。それが前の半分の距離（10フィート）に近付く時には、私の網膜上の角度は10°に増加し、2×の角倍率が生じます。もし代わりに物体がその元の距離の2倍(40フィート)に遠ざかれば、網膜におけるその角度の大きさは2.5°に縮み、角倍率は
×だけになります。しかし、これは20フィートの距離におけるその角度を参照しているだけなのです。だから、倍率をいうためには参照距離を与えなくては（仮定しなくては）ならないのは明らかであり、その参照角度の大きさから見たところの変化が光学的装置によって供給される角倍率なのです。この点はとても重要であり、そしてそれは依然としてよく誤解されます。
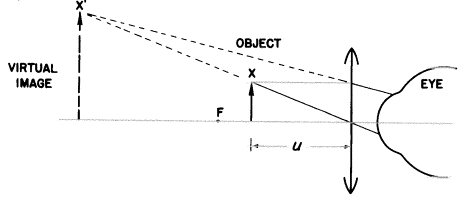
物体が無限遠にあって、角度で拡大された像が望遠鏡によって供給されると、無限遠上にある物体の角度が参照されるので、角倍率を計算するためにどんな固定した参照距離も詳述する必要は本当にありません。しかし、近くの物体を拡大するためには、あなたが見るように参照距離が必要なのです。プラス単レンズが拡大鏡としてどのように働くのか調べてみましょう。
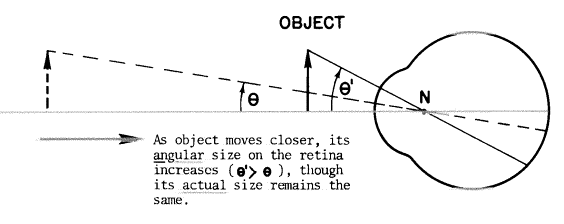
どんな物体がプラス単レンズの第1焦点内に置かれても、拡大された虚像で正立像が形成されます。そのレンズの後ろに位置した目はその像を見るでしょう。もしレンズからの物体距離uを調節すれば、像の大きさと位置も調節されるでしょう。レンズに対する目の動きは実際の像の大きさに影響しませんが、その見かけの（角の）大きさは変化するかもしれません。あたかも実際の物体に近付いたり遠ざかったりすることがその網膜像を変えるように。（下図の物体が目に近付くと、実際の大きさは同じであるのもかかわらずその角度は網膜上では増加（θ’>θ）します。）
私は（見かけの大きさに影響する）かもしれないという言葉を特に強調したいのです。なぜならそれは影響しないかもしれないからです！像がとても遠い距離に位置すると仮定しましょう。つまり、もし物体距離uがプラス単レンズの焦点距離に等しいのであればということです。それで、もし目がレンズに近付くか遠ざかれば（mmかyards）、その像の網膜上の角度は変化しないでしょう。あなたの目が像の距離と比較してレンズからかなりの距離だけ遠ざかったら変化するだけです。たとえばもしあなたが山から5マイル離れていてそれに数メートル近付いたら、これは目に見える山の大きさを本当に増やさないのとちょうど同じです。それを遂行するためにはあなたはたとえば
から
マイル近付かなければならないでしょう。その時だけあなたは網膜上の角度が増加するのに気付きます。ここでは同様に像は無限遠で、レンズを通して見続ける限り、それから遠ざかるに従ってその角度が小さくなるのを観察できないでしょう。
下図に示されるように、θ’はレンズに向き合う物体の角度です。θ’はいつもレンズに向き合う像の角度でもあります。
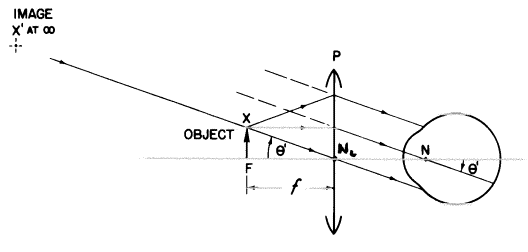
物体がプラス拡大レンズのFにある時、創造される網膜像の角度もθ’となるでしょう。私たちはこれをどのようにして知るのでしょうか？
そう、物体の先端Xから出た全ての光線はレンズの像空間において平行であり、レンズの節点を通る光線と同じ角度で軸を全てが交わらなければならないことがあなたには理解できるはずで、その角はθ’です。それらの像光線のうち1本は目の節点を通るでしょうから、網膜像の角度もθ’となるでしょう！そして、目がとても離れていてレンズPを通るXからの光線が瞳孔に入れなくなっていなければ、それはいつもθ’となるでしょう―レンズの屈折力ではなく直径に依存している状態です。
角度θ’は物体の大きさとレンズの焦点距離fに依存します。先ほどの図を勉強しましょう。fが短くなれば網膜像の角θ’は大きくならなくてはなりません。つまり、θ’はfに反比例し、あるいはもっと明確にいうとレンズのジオプター度数Pが大きくなるとθ’も大きくなるでしょう。私たちはまだ微少な角だけを扱っていることを思い出していただくと、tanθ’＝θ’であり、ゆえに、
しかし、レンズPがどれだけの“倍率”を生じるのかを決定するためには、この網膜像の角θ’と、同じ物体と関係しているいくつかの他の角を比較できなければなりません。倍率は網膜像がなにかよりも大きいか小さいことを示す相対的な言葉であることを思い出して下さい。だから、私たちの仕事は同じ物体を置く参照距離を見つけることであり、その例の中でその角度を決定し、その角度とレンズPによってできるθ’を比較するのです。あなたはその物体をどこでも好きなところに置けるので、いくつかの倍率の“数字”を得られます。その物体を置くところは（計算されたのではなく、任意に決められて）標準として同意されたものでなければなりません。
その標準となる距離はどれくらいがいいのか約数年間議論されましたが、ほとんどの目的では25cmに意見が一致し、この本や他のほとんどの教科書で使われています。しかし、40cmのほうがよい標準となる場合があることを知っておくべきです。たとえば、Louise Sloanの低視力者用の特別な視標の大きさは40cmの読書距離のためにM（倍率）単位で目盛りがつけられています。その位置で視力が弱い患者は読むように要求されます。もし与えられた大きさの印字がかろうじて読めるなら、その大きさの印字をさすM単位のラベルが検査者に直接ロービジョン用補助具の倍率を“表し”、それはその患者が最初に試みる有用なものになるかもしれません。
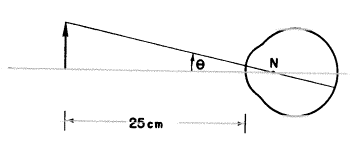
しかし、言いましたように標準的な参照距離は25cm です。視軸上の物体はそれが目から25cmの距離に置かれた時角θに向き合うでしょう。（次の図を見て下さい。）
私たちは今、レンズP―プラス単レンズの拡大鏡―によって供給される角倍率に戻ることができます。微小な角では：
θ’＝（物体の大きさ）・（レンズの屈折力）
そして θ
M
そして、倍率は物体の実際の大きさからは独立しているように見えます。
は私たちが選んだ標準距離を表します。もしもう1つの距離dが参照として使われるのであれば倍率はP×d(メートル)となります。
だから、私たちはプラス単レンズの拡大鏡の角倍率＝
と分かりました。だから、＋8Dの球面は2×の拡大鏡と呼ばれ、＋20Dの球面は5×の拡大鏡と呼ばれます。
同じ推論は目それ自身にも当てはまります。もし目が拡大鏡なしで25cmの参照距離に位置する物体を見たら、それもまた単位となる（1×）の角倍率を得るでしょう。もし同じ物体が今12.5cmに近付けられて、目がそれを鮮明に見るために必要にとされる8Dの調節ができるなら網膜上の角度は2倍になり、角倍率はこの接近と必要とされる調節によって2×となるでしょう。ゆえに、目の調節反応の増加はプラス単レンズの拡大鏡によって供給される倍率に加わることができます。
25cmの参照距離では、目の調節で与えられた拡大は
の比率であり、レンズによって供給されるものと同じです。だから、調節による拡大はレンズそれ自身によるものに直接加わります。単レンズによる可能な最大の倍率を決定するには、私たちは目の調節能力を考慮する一般的な表現を使います。その表現は
です。前の例では、それで+8D(2×の拡大鏡)のレンズがたとえば8Dの調節力を持った目と組み合わさった時、
、つまり全体で4×の可能な拡大効果を供給するでしょう。
臨床上の注意点：
上述の臨床上の重要な含蓄は、20フィートで視力が不良（約20/100）な児童は高倍率のプラス単レンズ拡大鏡（高いバイフォーカルの加入によって与えられるような）を読書用に使用する必要はめったにないでしょう。調節力は彼が読書用の材料を近くに持ってきて満足のいく拡大網膜像を得られるぐらいに普通は十分あり、レンズからそれ以上の補助を必要とはしません。Kestenbaumは低視力患者に必要とされる近見視用加入度のよい近似値は、彼の遠方視力の逆数であると指摘しました。視力が
であれば
、つまり＋5Dの加入度の補助が近くで作業する場合には必要です[1]。上に挙げた例の子供では十分な調節力があるので、この加入度は多分説明のように不必要になるでしょう。
＊ ＊ ＊
プラスレンズの拡大鏡から目を遠ざけるとレンズの角倍率は変わらず、網膜像の大きさが変わらない（物体が拡大鏡の前焦面にあると仮定します）ことは以前に私たちはお見せしました。しかし、目が遠ざかるに従って何かが変わりますが、それは視野です。目に見える像の範囲は目がレンズに接している時が最大ですが、目が遠ざかると減少します。
臨床上の注意点：
目の内部を検査するのに便利でちょっとした道具である直像鏡(direct ophthalmoscope)は目の光学的な構成要素を単純な拡大鏡として利用します。直像鏡自身はフラッシュライトだけであり、あなたが光線とともに観察できるように整えてあります。そのダイヤル上の全てのレンズはあなたの屈折異常、患者の屈折異常、あなたが及ぼす（しかし及ぼすべきではない）調節量、もしくはあなたが検査している眼底病変の高さや深さを補償するためだけにあります。これら全ての合計がゼロになるでしょうから、眼底をきれいに見るためには、あなたの直像鏡のダイヤルには補足レンズは不必要でしょう。だから、あなたは患者の角膜と水晶体の屈折力を結合してプラス拡大鏡として使っているのです。
私たちは正視眼のジオプター度数がおおよそ60Dであることを学びました。ゆえに、眼底検査の角倍率は
です。つまり、水晶体と角膜なしで眼底を目から25cm離して見るよりも、視神経乳頭（それは現実には約1.5mmの直径です）は直像鏡を通せばその大きさの15倍に見えます。
＊ ＊ ＊
私たちの心理的な仕組みは、私たちから物体の距離の変化を物体の角度の変化に代えることができるようになっていて、限界はありますが私たちはかなり自由にそのようにできます。ゆえに、さまざまな大きさで存在できる物体の像の大きさが網膜上で増加すると、私たちは物体自身が大きくなったのか、それが私たちに近付いてきたのかどちらかに知覚できます。通常私たちは後者が起こったと“感じ”ます。しかし、もし私たちがその距離を変えられなかったことを知っていれば、角度の増加は物体の拡大と解釈されるでしょう。
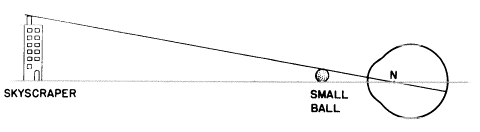
上図に示されるように、ボールと摩天楼両方とも網膜上での像の角度上の高さは同じです。ボールはどんな大きさにもなるので、その網膜像は心理的にその距離を調整できなくて、そのボールは近くて小さいのか遠くて大きいのかどちらかに“見える”かもしれません。しかし、建物はある大きさとして知られているので、変化するのは距離なのです。
摩天楼とボール両方ともに、距離をもっと正確にする手助けをする手がかりは、影、色、重なりなど以外には存在しないと私は仮定しています[2]。これらいずれの手がかりも（あなたの“心理的装置”も同様に）、本当に変わったのが距離か大きさなのかをあなたがはっきり選択するように決定付けることができます。望遠鏡と双眼鏡は典型的に物体を“近付ける”ように見えるのは、視覚化された物体の大きさを知っていて慣れているからです。一方顕微鏡はそのように物体本来の大きさに精通していないので、物体が“大きくなった”ように見えます。もちろん、これら全ての装置は物体の網膜像を大きくできるだけです。
だから、角倍率は（横倍率と対照的に）目やカメラに使われていて、像の真の大きさは間接的にだけ重要です。というのはそれは変数の1つであるだけで、その他にその距離があるからです。どちらかの実際の値を隠している1つのデータの中で“角倍率”という用語は両方の変数を考慮しているのです。どちらが見かけ上の大きさなのかという個人的な判断は多くの心理的要素の均衡によるでしょうが、私たちの課題である“角倍率”としては考慮するのは角度だけです。