�@��R�߁@�c�{��(Axial Magnification)
�@���{���Ɗp�{�������̃^�C�v�ɓ��Ă͂܂����1�̃^�C�v�̔{�����܂�����܂��B������c�{���ƌ����܂��B����͕W���I�Ȍ��w�̋��ȏ��ɂ͒ʏ�c�_����Ă��܂���B���͂����œ��ɓ|����ꌟ���@�Ɋ֘A���āA���̑��݂Ɠ��ʂȏd�v���ɂ��Ȃ����C�t���邽�߂ɂ�������������̂ł��B
�]�����ł͊ώ@�҂̒��߂ɂ�����ْ��͓���ɂ���ċ���������p�{����2���ɔ�Ⴗ�邱�Ƃ����Ȃ��͕������Ă��܂��B����͕��̂̎���i�擪�������܂ł́j�����i�܂�A���ꂪ�ߕt���ė��鎞�j�̔����ȕω����ǂ̂悤�ɂ��čŏI�I�ȑ��̈ʒu���g�傳�ꂽ����ω�����̂��𖾂炩�ɂ��܂��B�܂�A�ŏI�I�ȑ����ƂĂ��߂������A�䂦�ɂ���ɑ傫�Ȓ��߂�K�v�Ƃ��܂��B�������c�{���ł��B
���Ƃ����{���������Ă��鎞�ł��i���}�Q�Ɓj�i![]() �j�A���̂������ω��i��x�j�͑��������ω��i��y�j���`������ł��傤�j�B
�j�A���̂������ω��i��x�j�͑��������ω��i��y�j���`������ł��傤�j�B
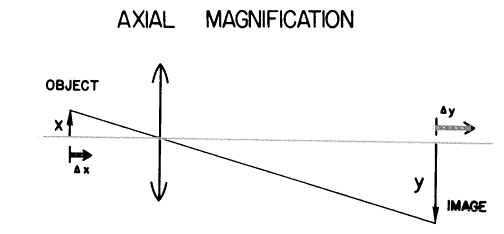
�����̕ω��i![]() �j��
�j��![]() �A�܂艡�{����2��ɔ�Ⴕ�Ă���̂ł��B�i����͎��̈ȑO�̘_����1�ɏڏq���Ă���A���Ƃ̓|�����̐߂ŗv���ł��傤�B�j������A�c�{�����p�{����2��ɔ�Ⴗ��悤�����{����2��ɔ�Ⴕ�܂�[1]�B
�A�܂艡�{����2��ɔ�Ⴕ�Ă���̂ł��B�i����͎��̈ȑO�̘_����1�ɏڏq���Ă���A���Ƃ̓|�����̐߂ŗv���ł��傤�B�j������A�c�{�����p�{����2��ɔ�Ⴗ��悤�����{����2��ɔ�Ⴕ�܂�[1]�B
�@�����ł��Ȃ����Ă��c�{���Ƃ����p����������ɕ�����Ȃ����Ƃ͂Ȃ��͂��ł��B