1. Badalの原理（“臨床医のための光学”，p264-p267より引用）

最初に、少し背景を言います―あなたが患者の調節近点を調べる時、彼に普通は検査カードの奇麗な文字を読むように言います。少しずつそのカードを近付け、その文字がぼけることを彼が認めるまで目に近付けます。これは臨床場面では実用的ですが、研究所で正確な測定をするには十分ではありません。というのは、カードが目に近付けば目の節点で文字に向き合う角度は大きくなるからです。ゆえにあなたは患者が同じ文字を見るのをより簡単にし、その最初のぼやけを認識しにくくします。

調節刺激を変化させ、それでもまだ網膜上の（角度の）像の大きさが変わらない方法があります。これが起こることを許す光学的原理はBadalによって発見されました。

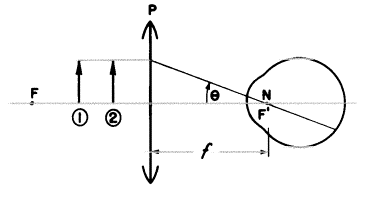
プラスレンズをその焦点F’が目の節点と一致するように目の前に置きます。物体がレンズの前に置かれますが、その第1焦点Fよりも近くにします。物体の端（末端が軸上にある矢印とします）は軸に平行な1本の光線を発するでしょう。屈折のあと、その光線はF’を通過するでしょう。F’は目の節点と一致していたので、光線は曲げられずに進むでしょう。節点における角は、その像が実際にはどれだけ遠くに位置付けられても、その目によって見られる像の角度をθにします。上の図では、物体が2の位置で作られた像は当然1の位置にある物体によって作られた像よりも目に近いでしょうが、物体の位置1と2両方とも目には同じ像の角度を作るでしょう。2にある物体に対応している像は、それゆえに、大いに調節を刺激します。だから、この光学システムでは像の角度が同じである一方、調節に対する刺激は変化することがあなたには理解できます。

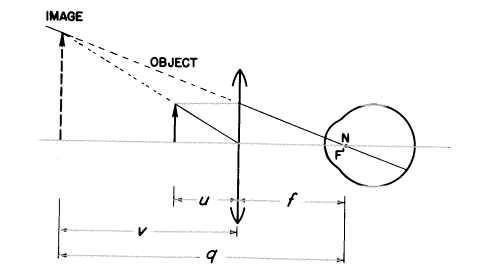
上のレンズPに関することでは、物体は距離uにあり、像は距離vにあります。U＋P＝Vに再び戻ってみますが、ここではUとV両方とも発散光線であり、そしてゆえに負（マイナス）です。

−U＋P＝−V

2項の表現（）は1つの分母uで組み合わせると、

だから、

それで、

そして、

では、この情報を目に関係付けましょう。節点Nから像までの距離は(v＋f)です。これを全体の距離qと名前を付け替えましょう。

q＝v＋f

この表現の中で、vにを代入し、fにを代入します。それで次の式に到達します。

組み合わせて、

分子の中で、(uP)と(−uP)は相殺され、

だから、目の節点からの像までの距離qは次のようになります：

その時、この像の目における発散光線Qは

ゆえに、Q＝uP²−P

　レンズP＝＋5Dで、物体がレンズPから5cm、u＝0.05mの特別な例を考えましょう。

　それで、 Q＝0.05(5)²−5

Q＝0.05(25)−5

Q＝1.25−5

Q=−3.75D

ゆえに、物体が＋5Dのレンズの前5cmにある時、目によって見られる像は3.75Dの調節を刺激します。これとuがとる他のいくつかの値は下のグラフに描かれ、そこではQとuは直線的な関係があるように見えます。ゆえに私たちはQはuと正比例であると言えます。

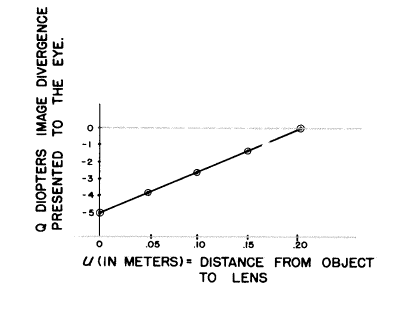
　この関係、Badalの原理は目における（つまり、F’で）像の発散光線Qは物体距離uに正比例することを示していて、また、上の例ではF’は目の節点Nに位置しています。しかし、私たちがレンズメーターを扱う時、私たちは視野レンズのF’を“未知の”レンズの頂点に置き、そしてuは視野レンズから十字線の的までの距離でした。2つの場合は正確に比較できることは明らかで、今あなたは何がレンズメーターの目盛りを線的にしているのか理解できます。 Q.E.D.（証明されるべきものでした）