第4節 物体空間 vs. 像空間
ときどき概念を扱う時には直感が定義よりもよいので、今まで、あなたにこれらの言葉を扱う“感じ”をあなた自身で私はつかんでもらいたかったのです。さて、しかしながら記録をきちんと整理するために、私はすでに自由に使っていた“物体空間”と“像空間”の2つの概念的な言葉を明確にしようと思います。しかし、今までにあなたはすでにそれらが何を意味しているのかうすうす気付いていたでしょう。
レンズに突き当たる前に物体面から出る全ての光線は“物体空間”に位置すると言われます。レンズがそれ自身の屈折力(vergence)をそれらの光線に加えたあと、合成された光の広がり(vergence)は“像空間”に存在すると言われます。それは十分簡単に聞こえます。それらの空間を作っているレンズは右にある“像空間”から左にある“物体空間”を 物理的に分けたように“見えます”が、そうではありません。両方の空間はレンズの両側に同時に共存し、そしてそれはこの概念を混乱させています。
物体空間はそれらがレンズに影響される前における光線と光線の方向のためにだけ存在します。物体空間がレンズにとってひょっとしたら物体の代わりになる全ての点で作られていると考えてみてください。私たちはレンズの左に置かれた実在の物体から来る発散光線について勉強したばかりですし、どのようにして収束した物体の光線がレンズの右に光学的に虚の物体を作るかも見ました。後者の物体もまたレンズの物体空間にあります。だから、私たちはレンズの物体空間は完全にレンズを包み込んでいることが分かります。そこで、覚えておいていただきたいのは、レンズの物体空間は実在もしくは虚の光線を含むかもしれませんが、それらはレンズに影響される前であるということです。
他方、像空間はレンズもしくは光学システムに影響されたあとの光線だけが存在するのであり、この空間はレンズがすでにその影響を物体の光線に働かせたことによってのみ存在するのです。像空間もまた完全にレンズを包み込んでおり、もし像がレンズの右にあるのならそれは実像であり、もし左にあるのならそれは虚像です。どちらのケースでも像はまだ“像空間”にあります。
全てのレンズは完全に―同時に―物体、像、両方の空間によって巻き込まれているということをあなたは今理解すべきです。みかけに反してこれらはあなたを混乱させるために作られたのではありませんでした。上述したことを心に留めておいてください。
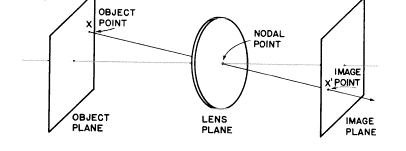
今まで私たちは軸上の物点と像点と図示されたそれらの共役関係を見ましたが、(軸上の焦点の議論を通して)点は面も表すということを詳しく述べました。これらの物体と像の面はそれらに対応する軸上点を含んでおり、レンズ面と平行であって、それらの点の(レンズ面における)光の広がり(vergence)の全ての特性を所有しています。それは軸上点を位置付けるのと同様に(U+P=V)、レンズに関係したこれらの面を位置付けます。1つの面のどの物点もそれと共役になる面の中にその像があり、それは物点Xから射出されレンズの節点を通るたった1本の曲げられていない光線によって示された明確な位置に存在します。
私たちはU+P=Vから何か他のことを学べるでしょうか?
もし私たちが2つの項を知っていれば3番目は簡単に計算でき、全ての種類の適当なちょっとした問題は扱いやすくなります。
例1
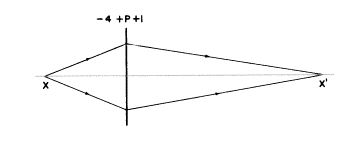
どれくらいの強さのレンズがその左側25cmのところに置いた物体の像を1m右にあるスクリーンに映し出すのでしょうか?
答え:
U+P=V
−4+P=+1
P=+5D
+5Dのレンズが式を満たします
例2
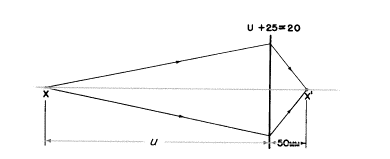
+25Dのカメラレンズの後ろ50mmに置いたフィルムに鮮明に像を映し出すためにはどれくらいの距離に物体を置かなければならないでしょうか?
答え: v=50mm=0.05m、そしてP=+25D
U+P=V
U+25=![]() (次の図を見てください)
(次の図を見てください)
U=20−25=−5D
u=![]() =−0.2m=−20cm
=−0.2m=−20cm
物体Xは(左に)20cm離れていなくてはならない。
例3
物体と像を1m離して置くためには、物体とそれに対応する像の間のどこに+4Dのレンズを正確に置かなければならないでしょうか?
答え: XとX’は1m離れており、uは物体の距離でvは像の距離です。(下の図を見てください)。
絶対値での距離の測定(符号には関係なく)では、u+v=1mなので、v=(1−u)mとなります。
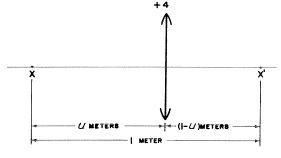
レンズが物体と像の間にあるので、たとえどんな距離uが存在しようとも、物体の光の広がり(object vergence)Uはレンズ面ではマイナスでなくてはなりません。同様に推論すると、Vはプラスに違いありません。
だから、U=![]() とV=
とV=![]() となります。
となります。
ここで、私たちの一般式U+P=Vにこれらを代入します。
U+P=V
![]()
この方程式をuについて解くためには、私たちは分母を削除することによってそれを簡単にしなくてはなりません。この手作業は中学3年生の簡単な代数を必要とします。
−(1−u)+4(u)(1−u)=u
−1+u+4u−4u2=u
−1+4u−4u2=0
−1を掛けると 4u2−4u+1=0
(2u−1)2=0
平方根をとると 2u−1=0
2u=1
u=![]()
1−u=v=![]()
ゆえに、レンズは物体と像の両方から50cmのところに位置し、つまり、それらの真ん中になります。[1]
例4
左に置かれたプロジェクターからの収束光線が鮮明な、直径3cmの点状の像を右にあるスクリーン上に作ります。あなたは点の大きさを気にする必要はありませんが、プロジェクターを動かさずに右25cmのところに像を持っていきたいのです。あなたを助けるために役に立つ−2Dのレンズをあなたは持っています。あなたは像を置き換えるためにこのレンズをどこに持っていかなくてはなりませんか?
答え: XからX’の距離は0.25mです。
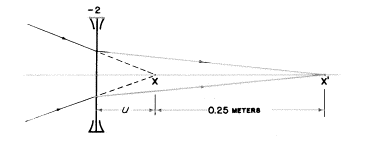
uを私たちのレンズから像X(それはもしレンズが最初に光線を横切っていなければプロジェクターによって産出されたものです!)までの距離としましょう。これは私たちの−2Dのレンズに対する物体の距離です。物体の光の広がり(object vergence)はU=![]() 、P=−2、像の光の広がり(image vergence)はV=
、P=−2、像の光の広がり(image vergence)はV=![]() ですので、
ですので、
U+P=V
![]()
(0.25+u)−2(u)(0.25+u)=u
0.25−0.5u−2u2=0
−1を掛けて 2u2+0.5u−0.25=0
因数分解すると (2u−0.5)(u+0.5)=0
つまり、問題には2つの答えがあります。
a) 2u=0.5
u=0.25m
u=+25cm
b) u=−0.5
u=−50cm
私たちはこれらの答えをどのように解釈すればいいのでしょうか?
a) −2レンズは元のスクリーンの前25cmに置かれないといけません。こうすると25cm離れた位置に投影された像を動かせます。
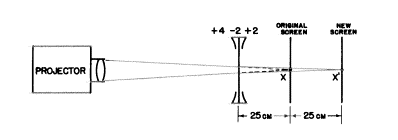
b) しかし、私たちは代数学的な解法から、もう1つの可能性を示唆されました(下図を見てください)。−50cmの物体距離uは、レンズに対し発散光線を送るようにレンズを置くことになります。これは私たちが映写機の像がXに作られたあとの光路にレンズを置いた時のみに可能です。この位置にスクリーンがない時光線は進み続けるでしょうが、その時それらは発散するでしょう。−50cmに置くと、−2Dのレンズは−2Dの光の広がり(vergence)を“見て”、−4Dの像の光の広がり(image vergence)を作ります。理由は、
U+P=V
−2+(−2)=−4
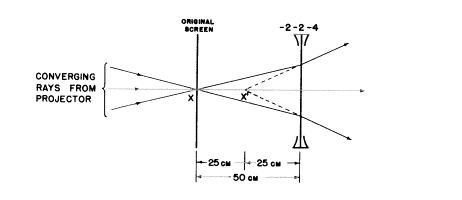
像の光の広がり(image vergence)−4は、私たちのレンズが25cm左に位置する虚像を作るということです。
本来の物点Xは最初の問題で述べた条件のように、確かに25cm右のX’に像を映しますが、もちろん私たちは数学的解法が最終的な虚像を含むことを先験的に知る方法がありませんでした。この答えが像の基準を満たしていようとも、付加した収束レンズなしにこの像を結ばせることは不可能ですから、この答えは実用的な解法ではなく、答え(a)が正しくて実用的なのです。
他の練習問題
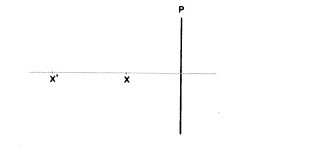
もし、私があなたに上記の状態でどんなタイプのレンズ(プラスかマイナス)が軸上点Xの像をX’に結ぶのかを私に答えるように求めたら、あなたは答えることができるべきです。もしあなたができないなら、私の推論に従ってください:XがレンズPの左にあるので、光線はレンズに向かって発散するでしょう。レンズによって影響(屈折)されたあと、Xからの全ての光線はそれらがX’からきたかのように曲げられるに違いありません。だから、Xから任意の光線を引き、それがX’からきたかのように見えるためにどれくらいレンズがそれを曲げるのかを知るのです。もし、それが光線を収束させるのであればレンズはプラスでなければなりません。もしそれが発散させるのであれば、レンズはマイナスでなければなりません。
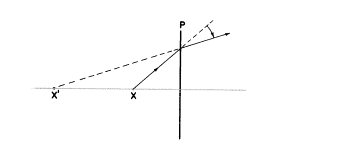
ここでPは光線がレンズの軸に向かって下方に曲げられますからプラスでなければなりません。つまり、収束がレンズによって加えられるのです。付加された収束はしかしながら実像の点を形作るのには十分ではありません。X’はよって虚像です。
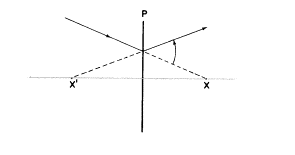
XがレンズPの右にあるとしたらどうでしょうか?
右にあるXのただ1つの違いは、光線が物点X(つまり虚でなければなりません)に向かって(レンズ面において)収束していることを示していることです。Xに向かって引かれた光線がレンズPに当たったあと、それはあたかも軸上点X’からやってきたかのように振る舞うでしょう。再びレンズのところでその1本の光線になにが起こっているのかだけに注意してください。光線は軸から離れるように上へ曲げられ、発散がそれによって加えられたに違いありませんし、ゆえにここでPはマイナスレンズでなけらばならないのです。この例ではXとX’は両方とも虚です!
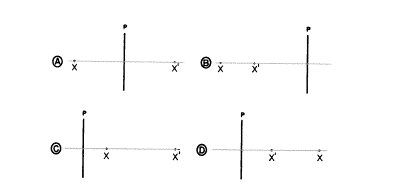
他のいくつかのレンズにプラスかマイナスをつけてください。
答え:A.プラス B.マイナス C.マイナス D.プラス