第１節　ガリレイ式光学システム

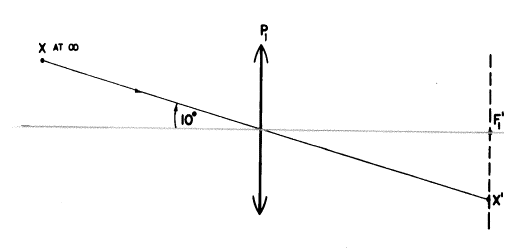
　前述した図では、無限遠にある物点からのゼロの光の広がり(vergence)は同様にゼロの像の光の広がり(vergence)となってシステムから出ていくことを示しています。これは無限遠にある全ての物点で真実ですが、その図は軸上にあり無限遠に位置するある特定の点からの光線だけを示しています。では軸外にある無限遠上の点、たとえば水平の上の10゜ではどうでしょうか？

　私たちの最初のレンズP₁は第2焦面にこの点の像を映します。物体は無限遠ですが軸外ですので、像点はP₁の節点を通るXからの光線で決定されます。

　私たちはXからの光線をあと2、3本引くことができます。

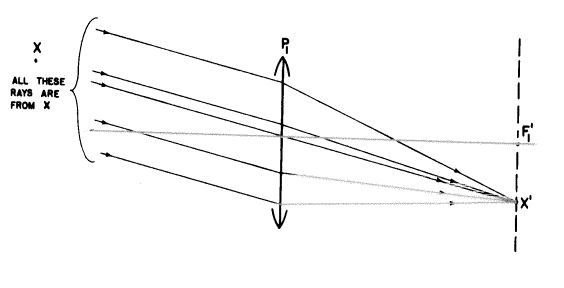
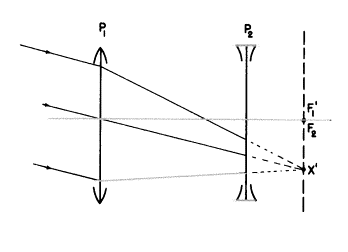
Xが無限遠ですので、レンズP₁に到達する光線は全て平行でしょうし、全ては軸に対し同様に10ﾟの傾きがあるでしょう。そして、P₁で屈折したあと全ての光線は第2焦面にある像点X’へと曲げられるでしょう（私たちが最初の章に戻って見たように）。しかし、ガリレイ式中和システムではP₁の像空間におけるこれらの光線は実際にはX’に到達できません。それらはP₁の第2焦面前に置かれたマイナスレンズP₂で最初にさえぎられます。

　P₂はX’を“物点”として“見て”その像を映し出します―問題はどこにあるのでしょうか？私たちはP₂の物体空間にX’があって、P₂の第1焦面に位置していることを知っています。（P₁のF’とP₂のFが一致していることを覚えていますか？）それで、P₂によるX’の像は無限遠でなければならず、最初X’に向かっていた全ての光線は平行光線束でP₂を去っていかなければなりません。

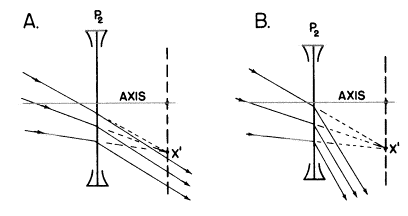
　今までのところはうまくいきました。しかし何度でこれらの光線が出ていくのか私たちはどのようにして知るのでしょうか？それらはどの方向にも曲げられるでしょうし（下のAとBには2つの可能性が示されています）、まだそれらは平行光線のままでしょう。

　これらの平行光線束に与えられた最終的な方向を私たちはどのようにして求めるのか分かりますか？やってみましょう。起源となる物点Xからの全ての光線はP₁によってX’に像を映し出されなければならなかったことを私たちは知っています。ゆえに、私たちは元々X’に向かっていたどんな光線も逆にたどることができますし（下図の1、2、3のように）、それら全ては、10°の傾きを軸に対して持つ元々の物体光線―P₁の節点を通る“鍵”光線と同じ―全てに平行でなくてはなりません。

（光線3をX’からP₁に逆に引くには、3がP₁と“交差”してその方向を変えるために人工的にレンズ面P₁を上に引き延ばさなくてはなりませんでした―レンズP₁の物体空間の中ではその光線も軸に対して10°の角度をとっています。）

　どんな場合でもP₂の節点を通ってX’から逆をたどる1本の光線（光線2）があって、そうする時は曲げられないことを私たちは分かっています。そうです！その光線2は物体をX’としたレンズP₂からの像を映し出す全ての光線の最終的な方向を決定する1本となるでしょう。その角度の方向は下図にθ’として示されています。

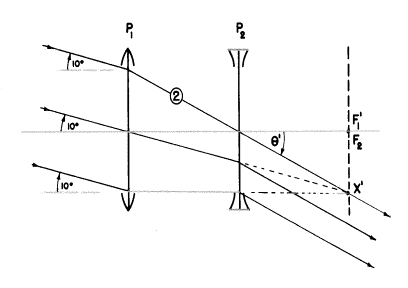
　要約すると、もともと物体Xから出た光線2は軸に対して10°の角度でP₁に当たっています。P₁はX’に向かってその光線を屈折します。この光線はP₂によって遮られますが（そして、ゆえに無限遠となるX’の最終的な像に関係するでしょう）、それはP₂の節点を通る1本の光線なのでそれ以上は曲げられません。私たちは今その方向が分かっていますから、像に映し出される最終的な全ての光線の方向も分かります。

　（ところで、最終的な像光線はそれに対応した物体光線よりも“密”に詰められているかのように見えます。多くの人は像の縮小がこの“密”を引き起こしたに違いないという誤った結論に導かれます。迷ってはいけません。全ての像光線は物体光線と同じ点から生じます。ゆえにそれらの見かけ上の密度は拡大や縮小を意味することはできません。拡大の決定に関して重要なのはそれらの角度と方向の変化だけなのです。

　私たちは上図を簡単にして、10°傾いたたった１本の物体光線と明らかに10°よりも大きいθ’で傾いている１本の（曲げられていない）像光線を示すことができます。元の物点Xの最終的な像は無限遠になるでしょう（というのは最終的な像空間に平行光線束があるからです）が、その像は元の物点の傾きである10°よりも軸に対する傾きが大きく見えるでしょう。

　P₂の後ろに目を置いて、この無焦点の“中和された”レンズシステムを通して最終的な像点X’’を見るなら、目が何を見るのかは明らかです。X’’は水平線の上方にXよりも大きな角度を取るので、より大きく見えるに違いありません―その角度で拡大されるのです。このレンズシステムはガリレイ式であり、つまり陸上の望遠鏡です。見られる像は虚像で正立像であり、マイナスレンズのほうが目に近くなっている時はいつでも拡大されます。

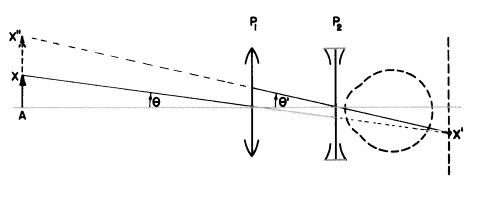
　自分で図を書いて、もしプラスレンズのほうがあなたの目に近いならば、像は小さくなることを説明してみましょう。（この後者の無焦点縮小システムでも、プラスレンズの屈折力はいつもマイナスレンズよりも小さくなることは明らかでしょう。）

　上に示したガリレイ式拡大システムがない場合は目は物体AXを見るでしょう。この望遠鏡を使うと目はそのより広い範囲の網膜面を占める像AX’’を見るでしょう。実際の拡大はもちろんθ（物体の角度の大きさ）とθ’（像の角度の大きさ）の関係に依存します。この角倍率Mはです。

　もしθ’がθの2倍であれば、角倍率は2、つまり2×となります―見かけの大きさが100%増加することを意味しています。

　では、私たちが“中和”しているレンズの屈折力を知っているなら、望遠鏡の角倍率をどのようにして表すのかを見てみましょう。もう一度簡単にすると、ただ1本の物体光線ともう1本の像光線がX’に引かれます。像X’は軸から距離hのところに置かれます：

　

微少な角ではtanθ＝θ、tanθ’＝θ’ですから、

　　　　　　　

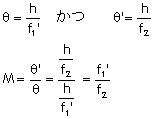
あなたがあとで天体望遠鏡の拡大システムを勉強する時に見つけることとは対照的に、ガリレイ式システムでは物体とその像の両方は正立像であり、だからθとθ’の両方は同じ方向（ここでは、時計方向）に測られます。ゆえに、それらは同符号です。しかし、これを達成するには、P₂をマイナスレンズ（マイナスのf₂を伴っている）にしなければならかったので、私たちの一般的な表現は次のようになるでしょう：。これはお互いに“中和”する任意の2つのレンズ間の基本的な拡大関係です。今もしP₂がここにあるようにマイナスレンズであったなら、Mはプラスになり正立像を表すのは明らかでしょう―それは元来慣習で合意しています。