1. “軸外”の物体と像

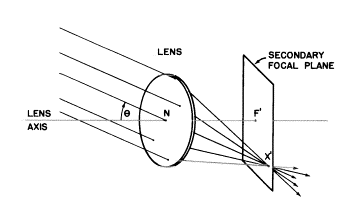
　物点Xが無限遠にあってもレンズの軸からはずれて上方に位置すれば、そこで生じる光線もまた平行の束でレンズに到達しますが、軸に対してある角度（傾き）でレンズに当たります。どれくらい急な角度なのでしょうか？想像してみてください。これらの平行光線の傾きθの角度はレンズの節点にまっすぐ入射した、点Xからの1本の光線によって与えられます。もちろん像は第2焦面(secondary focal plane)に位置しますが、それはその面が無限遠にある物点を表す全ての像点の場所だからです。その面の像点の正確な位置は、レンズの節点を通して曲げられていない光線によって正確に示されます。（次の図を見てください）

　

　もしカメラのフィルムが第2焦面に位置し、レンズPが単純なカメラレンズであったなら、光学的無限遠に位置する全ての物点の鮮明な像はフィルム上に作られ、子孫のために残されるでしょう（もしフィルムが適切に露出を与えられていたなら）。

　前述したことを今続けますが、レンズPに物点Xを近付けていきましょう。すると点Xは第1焦点Fよりもレンズに近付いていくでしょう。Xがレンズから25cmの距離になったとしましょう。すると、

　　　　　　　　　　　　　　　U＋P＝V

　　　　　　　　　　　　　　−4＋3＝−1

　レンズPにおける像点の光の広がり（vergence)は−1Dです。

ここで像点の負の光の広がり（vergence)に初めて私たちが出会ったのです。これはどのように解釈されるのでしょうか？

　慣習により、私たちはマイナスが物体や像の発散光線を意味することに最初に同意しました。そこで、ここでもまた私たちはこの慣習に従って、マイナス符号は発散光線がレンズを過ぎ去ってから“像空間”の中にあることを意味しなければなりません。これらの光線は発散しているので、それらはスクリーン上の焦点にたどり着くことはできません。像の収束光線だけが前に言ったように実像を形作ることができるのです。私たちは（定義によれば）もし発散光線が“像空間”にあったなら、像は虚像であり、それはスクリーン上に焦点を結ぶことができません。たとえそうであっても、物点Xと共役である（対応する）像点X’がまだ存在します。しかし、像はレンズの左に位置します！どれくらいの距離でしょうか？そうですね。

　　　　　　　　　　　　　　U＋P＝V

　　　　　　　　　　　　　−4＋3＝−1

　　　　　　　　　　

　ゆえに、像点X’はレンズの左100cmのところにできるでしょう。

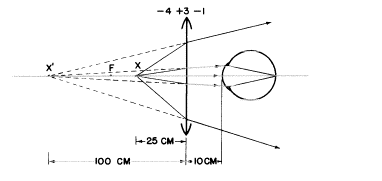
つまり、たとえ実在する光線（実線で示してあります）がレンズPを去った時発散していても、それらは100cm離れた実在する点からやってきた光線（点線で示してあります）であるかのようなふりをします。全ての実在する本当の光線は、この本の図の中では実線で示されるでしょうし、一方見かけの（虚の）点からの光線は点線で示されるでしょう。

　それで事実上、光線はレンズを過ぎてからあと、X’から発しているかのように見えるでしょう。つまり、レンズPを通して見ている目は点X（それはレンズから実際に25cm離れている）を“見る”のではなく、あたかもそれから100cm離れて位置しているかのように像点X’（レンズによって作られた点）を“見る”のです。

　もしあなたがX’から来たかのように見えるそれらの光線の目における光の広がり（vergence)を知ろうとするなら、X’と目の間の距離を決定しなくてはならないでしょう。目がレンズから10cmの距離に位置しているとしましょう。そうするとX’は目から110cmの距離に位置しなければならず、X’は目において、つまり、−0.91Dの光の広がり（vergence)を持ちます。X’はレンズPによって作られた像点であるだけでなく、同時に目のための物体でもあり、つまり、目の“物体空間”の中にあると言えることに注目してください。（たとえ、私がすでに“物体”と“像”空間という言葉を流ちょうに使っていたとしても、まだそれらの定義をもう少しあとまで保留しておきたいと思います。）

　この＋3Dのレンズのために最後の1例を考えてみてください：

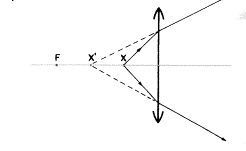
XはPに近付き続けます―それからたった5cmの位置まで―。Xはレンズに対して、つまり−20Dの光の広がり（vergence)Uを送るのです。

　　　　　　　U＋P＝V

　　　　　 −20＋3＝−17

　像X’は今、つまりレンズの左−5.9cmに位置します。さらにXをレンズに近付ければ近付けるほど、XとX’間の明白な分離は小さくなります。