第３節　回折

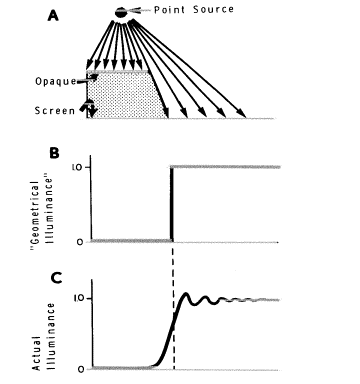
回折は見かけ上“角で曲がったり”、もしくは像か影の部分に現れる光の能力で、そこでは幾何光学的推論を厳密に使用する人はそれを予想しないでしょう（図5）。

図５.“ナイフの刃”による光の回折。A.点光源からの光は不透明な刃によって妨げられ、影がスクリーン上にできます。B.理論的なグラフ、スクリーン上の“幾何光学”的な像の明るさ。C.スクリーン上の実際の回折による明るさのグラフ。

　もしあなたが光の微小な波長に比較して大きな開口と距離を考慮するなら、回折効果は無視できます。ゆえに、もしあなたが光の巨視的な効果―レンズシステムの焦点調節効果もしくは目の光学的な構成要素、物体−像関係―を考慮すれば、これらは厳密な幾何光学の用語とスネルの法則に基づいた光の屈折でかなり適切に記述できます。しかしながら、光の“微視的な”側面を考慮した時（たとえば、網膜像の明るさのより鮮明な詳細）、回折が考慮されなければなりません。光が目の瞳孔のように大きな開口を通って通過する時でさえ、実際には網膜像はその光源の回折像です―光は網膜上に到達する前に瞳孔を“無理矢理通らなければ”ならないのです。

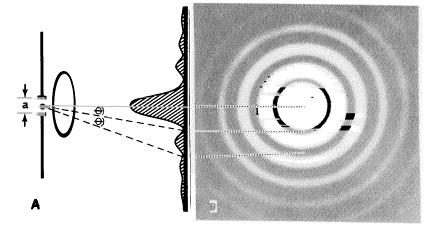
　小さな光源の回折像は、明るく、規則的に一定の間隔があり、強度がそれぞれ減少している連続した輪に囲まれた中心の“強烈な点”が見られます（図6）。もし光源が点ではなく長い物体であれば、物体を作っている全ての点に対応する回折像があります。

図6. 円形開口による回折。A. 図で表した回折パターンの強度。B. 実際の回折パターンの写真。a, 開口の幅。θ,“強烈な点”の中心と最初の暗い輪との間の隔たりの角度で、連続する暗い輪のそれぞれの間隔の角度でもあります。強烈な点の全体の幅は2θです。

　回折は不透明な物体のそばを光線が通過する時にだけ起こり得ます。ゆえに私たちは絶えずどんな光学的装置でもその効果に気付き、そこでは光はほとんどいつも開口によって妨げられています。それらによって産出される回折パターンは像の限定的な鮮明さを決定するでしょう。瞳孔のような円形開口では、“明るい点”の中心と最初の暗い輪との間の角度θ（ラジアン）は連続する暗い輪のそれぞれの間隔の角度に等しいのです（図6A）。

　θ＝1.22

ところで、θ＝開口の中心部の角度（ラジアン）

　λ＝光の波長

　　また、a＝開口の直径（単位はλと同じ）

回折パターンは瞳孔の直径がより小さければ明らかに大きくなり、瞳孔が約2.5mm以下になると視力的な重要性が生じます。（視力は実は1mmのピンホールを通して見た時には、ピンホールによる回折効果のためにいくらか減少します（pp.158-159を見てください）。）

　大きな開口やスリットでさえ、もし像（もしくは影）の光の模様の端が高倍率で詳細に調べられたら、回折効果に気付けます（図5を見てください）。

　円形開口と対照的に、もし1つのスリットが光を回折しスクリーン上に像を形成すれば、見える線の隔たりの角度は（ここでaはスリットの幅）となるでしょう。1.22は円形開口を扱う時だけ必要な定数なのでここではなくなっています。その時、規定のスリットの幅に白色光が入射すると（プリズムで起こるように）、含まれたさまざまな波長がおのおの異なった量で広がり、一番短いものは最小に曲げられ、最長のものは最大に曲げられるのが見られます。この広がりはプリズムの分散とは反対方向であり、そして、ここではその広がりは実際の波長λに線的に比例していることに注意してください。そしてもし多重スリットが単一スリットの代わりに利用されれば、個々の波長はもっと効果的に広げられ、強化されます。これはいわゆる回折格子であり、そこではとてもきれいで緻密に引かれた線がガラスに作られています（1インチに10,000から20,000本）。ここでは干渉と回折の両方の効果が構成され、有用な装置の中で共に作用します。回折格子は、異なる金属が化学的内容物について分析される定量分光学のような、さまざまな光学的目的のために使われます。