第８章 角度の測定
高校の幾何学と三角法では、あなたは角度を測るための異なる単位である、度とラジアンを与えられました。斜視の分野を学んでいると、あなたはあと3個の単位に出会うでしょう。それはプリズムジオプター（ただ1つの重要な単位です）、セントラドそしてメーターアングルです。手短にこれらの単位を復習することは有用でしょう：
a)
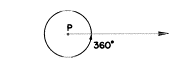
度―１点の周りにおける全体の角度の
として簡単に定義されます。
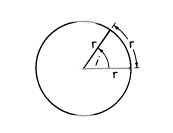
b)
ラジアン―どんな半径でもいいので円を作り、中心から2本の半径を引きます。
円弧の実際の長さが半径の長さに等しい時、その時の円弧に対する角iが1ラジアンとなります。
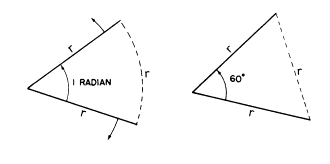
もし円周が糸でできていて、ぴんと張った半径の端がそれに固定され、含まれた角が1ラジアンであったなら、糸がぴんと張ってまっすぐな線となる前にいくぶん角iが増えるのが分かります。この点にたどり着いたら、“まっすぐに伸ばされた円弧”はやはり半径の長さに等しいので、もちろんその時iは60°となります。これは正三角形（それぞれの角度は60°です）を作ります。だから、1ラジアンの大きさは60°未満に違いありません。どれくらい小さく、そしてどのように正確な等値を求めるのかを見てみましょう。
どんな円でも半径の長さが（端と端をくっつけると）いつも円周を完成させる定数があります。その数値は2πです。つまり、（2π）の半径が360°の完全な円周を作ります（C＝2πrを覚えていますか？）。円周に沿って測られたそれぞれのrは中心角の大きさの1ラジアンを表し（“ラジアン”の定義）、また、1周した円周には2πの半径があるので、360°に等しい角度の大きさである2πラジアンがなければなりません。2πラジアン＝360°なので、1ラジアンは360°を2πで割った値（約57.3°）に等しくならればなりません。そして、逆に1°は
ラジアンに等しいです。私たちがこの単位を深く暗い過去から引きずり出してきた理由はまもなく明らかになります。
c)
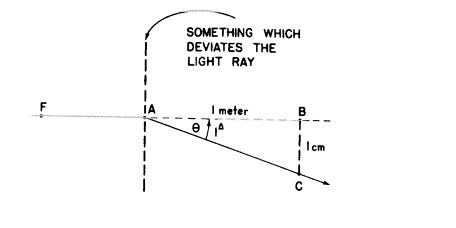
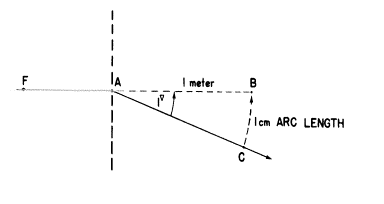
プリズムジオプタ−：1mの距離で1cmの明白な置き換えに対応する角度
光線FAは（いくつかの光学的装置に出会ったあと）“まっすぐな”道筋から角度θでCに向かって向きがそらされます。三角形ABCは直角三角形なので、tanθ＝
。
定義により、θ＝1△（プリズムジオプター）の時
BC＝1cmとAB＝1m
ゆえに、tanθ＝
同じ理由で、もしθが5△であればtanθ＝0.05
今あなたは反対もまた真であることがわかるでしょう。つまり、どの角θでも100tanθはプリズムジオプターでの角度に等しいのです。だから、角度からプリズムジオプターへの変換（逆も同様）は角度の正接に結びついていますが、ここで問題があります。表1を見てください。それは度によるθとtanθ（標準的な関数表を参照）とプリズムジオプターの関係を表しています：
表１
100tanθ
角度 tanθ （プリズムジオプター）
小さい角度では1°は1.7△に等しく、より大きな角度では（そうですね44°と45°の間では）1°は3.5△に等しい！どんな自尊心のある単位が目盛りに沿ってその大きさを変えるのでしょうか。つまり、プリズムジオプター（100tanθ）は本当の単位ではないことが明らかです。それは度（それはもちろん本当の単位です）と比較してその大きさを変え続けるのです。
私を間違えさせないでください―プリズムジオプターは有用な“単位”ですが、小さな角度を測るためだけのものです。典型的な臨床現場の中で、あなたがたとえば内斜視を測定している時には、通例約30°までの角度を扱うのです。0°から30°までのこの範囲内では1°は約2プリズムジオプターに等しいのですが、この推測は実はかなり正確です。しかし、大きな角度においてこの近似値を使うことでもたらされた誤差は大きいことを心に留めておいてください。45°を越える角度を扱う時には“単位”は急速に無意味になっていきます。
d) セントラド（▽）は、1cmの長さの置き換え（1mにおいて）がまっすぐの線分の代わりに円弧に沿って測られることを除いて、プリズムジオプター同じです。小さな角度ではセントラドはおおよそプリズムジオプターと同じです。
もうセントラドは忘れましょう。それは流行遅れで一般にはもう使用されていません。
e) メーターアングル：この角度の測定もまたあまり重要なものではありませんが、調節とその共同運動である調節性輻輳の間の比率の決定に関係する斜視の文献の中で見かけます。つまり、
の比率です。（プリズムジオプターはこの目的の単位としてはもっと適しています。）
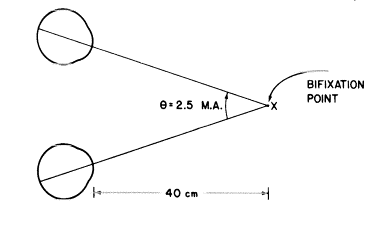
どのようなケースでも近付いた物体が目によって注視された時、2つの眼軸間の（輻輳の）角度はメーターアングルで与えられます。
もし目が点Xに輻輳し、目からXまでの距離が光の広がり（vergence)のジオプター度数で与えられるなら、角θは自動的にメーターアングルで表現されます。だから、もしXが40cmであれば角θは2.5メーターアングルです。
角θ（もしそれが度もしくはラジアンで表現されていたなら）は目からどれくらい離れているかによるので、この“単位”もまた真の単位ではありません。つまり、真の角度は瞳孔間距離（p.d.）に依存すべきなのです。もしp.d.がここに示したよりも大きかったら、θは実は大きくならなくてなならないのですが、それはまだたった2.5メーターアングルでしかありません！“メーターアングル”の使用は実際のp.d.を考慮することは避け、そしてこのことはこの“単位”の長所でもあり短所でもあることが明らかになります。
私たちはこの用語なしでもかなり快適です。
ここでの角度測定の単位に関するこの余談の必要性に学生は質問するかもしれません。その弁護に、私は全ての読者に各々の単位を理解してほしいだけでなく、これでラジアンに関する知識に関して同じ基準で始められると思ったのです。
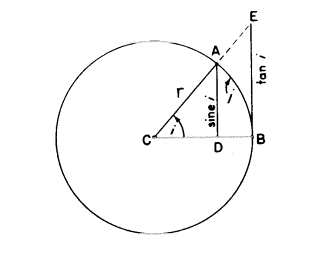
私たちはすでに中心角i（下図に示すように）は度もしくはラジアンで表現されることを示しました。対する円弧もまた、中心角iの大きさに正確に等しいので、その大きさは度、もしくはラジアンのどちらででも与えられます。（つまり、円弧そのものがたとえば45°、もしくは0.75ラジアンに等しいと言えます）。しかしながら、円弧iの長さの実際の測定（インチもしくはメートル）は明らかに半径の長さによるのです。同じ中心角では、半径が長くなると、円弧iの長さも長くなります。もし角iが1ラジアンであれば円弧iは半径の長さに正確に等しいのです。もし角i＝0.5ラジアンであれば円弧iは半径の2分の1に等しくなります。つまり円弧iはいつも中心角i（ラジアン）×半径の長さなのです。
私たちはCを中心にした円、半径CAとCBを描いて、半径CBに垂直な線を決めます。1つは半径CAの端から降ろし、他方は半径CBの端に降ろします。
sin i ＝
tan i ＝ 
もし私たちがいろんな長さの“単位”の1を使い、r＝1と仮定したら
ゆえに、 sin i ＝ AD
また、 tan i ＝ EB
言い換えれば、線分ADとEBはそれぞれ角iの正弦と正接の長さの表現です。
私たちが見てきたように、上図の円弧ABはi（ラジアン）×半径の長さに等しいのです。半径は1に等しいので、円弧の長さABは角iに等しくなります。
図から、これらの3つの長さを大きさの順に並べると：ADは一番短く、それから円弧AB、そして一番長いのがBEとなります。よって、代入すると
sin i < i < tan i
あなたは今角iが減少するに従い、何が起こるか想像できるでしょう。これらの3つはお互いにほぼ等しくなります。だから、比較的小さな角ではi（ラジアン）はsin i やtan iという三角法の表現の意にかなう代用品なのです。どれくらい小さな誤差がそのような代用によって生じるのか、表2を私は作ってみました。
表２
sin i の代わりに tan iの代わりに
i sin i i tani i(ラジアン)の使用 i(ラジアン)の使用
（度） (関数表より) （ラジアン） （関数表より） による誤差（％） による誤差（％）
---------------------------------------------------------------------------------------------------------
1° 0.01745 0.01745 0.01746 0.00% 0.01%
2° 0.03490 0.03490 0.03492 0.00% 0.01%
10° 0.17365 0.17450 0.17633 ＋0.49%
−0.104%
20° 0.34202 0.34900 0.36397 ＋2.01% −4.12%
30° 0.50000 0.52350 0.57735 ＋4.5 % −9.35%
40° 0.70711 0.78525 1.00000 ＋11.1% −21.4%
この表はi（ラジアン）がいろいろな角度の大きさで sin i とtan i の代わりになった時に生じる誤差の百分率を示しています。3つの点が明らかになります。
1) iはおおよそ20゜までの小さな角度ではsin iとtan iのすぐれた代理になります。たとえ、20゜でもsin iに変わった時はたった2％の誤差、そしてtanｉでは4％の誤差です。
2) iはいくらかtan iよりもsinｉのほうのよりよい代理となります。
3) sin
iのかわりにiを使うと、近似値はかすかに大きくなります。tanｉの代わりにｉを使うと、それはかすかに小さくなります。（これもまた先の図、特に線分AD、円弧AB、線分BEの長さを見れば明らかです。もし、あなたがこれらの線を比較するならば、あなたはsin iとtan iの近似値iの図式化された説明が得られるでしょう。）
私たちはまだ他の方法でもこの近似値を調べることができます。角iがラジアンで表されていれば、sin iの値は数学の“三角法の展開”で求められたsin iの数学的同値である iの値に単純に代えることで求められます。（ところで、これは関数表自体が作られる方法です。）目をつむらないでください！それは恐ろしいものではありません。展開は次のようになります：
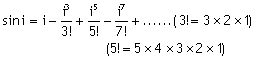
また、
だから、私たちはsin iもしくはtan iの値を正確に、そして私たちが望むだけ小数点以下の位を求められるのです。問題は合理的に正確であるには（sin iの代理として）
の項がどれだけ使われなけばならないかということです。表2に示したように、明らかな答えは、もし小さな角度のｉに限定すれば私たちは初項以外の項を取り去ることができ、sin iが角度iそれ自身に等しいと記述することでほとんど間違いはありません（iがラジアンで表示される場合）。これはいわゆる１次光学で扱う近似値です。それはπの代わりに近似値3.1を使うことに似ており、もしもっと正確な値が必要なら3.14のようにもう1つの項を加えられます。同様にして、sin iの値をもっと正確にする必要があるのなら、あなたは第2項の
を含むこともできます。
光学的な計算でsin iのためにもっと正確な値（ｉ−
）を使う時、私たちは“3次”光学を使っています―“2次”はないことに注意してください。tan iの正確さを増やすために、同様の項もまた加えることができます。sin iとtan i両方の正確さのために加えられた度はレンズのいくつかの収差の説明のために必要です。天文学者は星の位置の正確な計算のために5次もしくは7次にもなる光学を必要とするかもしれません。しかし、私たち臨床医にとっての重要な点は、ここで私たちが学ぶ全てのことについては、sin iの代わりは第1項の(i)だけが必要なのです。
1次光学は物体と像光線―近軸光線と呼ばれます―の評価を含み、それは屈折システムの軸の近くにあって、そのために入射角と屈折角は比較的小さいのです。私たちはある原理を詳しく述べるためにこの本の中で大きな角の図を使うという事実にもかかわらず、まだ近軸光線でレンズの作用を正確に記述しているだけだということを理解しなければならないのです。
あとで私たちが曲面屈折を扱う時、sin i の代わりにiを用いるでしょう。スネルの法則はni＝n’i’と簡単になるでしょうし、それは私たちがとても大きな角を扱わず、iをラジアンで表す限り正確です。