第２節　近視矯正

　遠視における遠点の矯正について言ったことは全て近視についても言えます。どんな矯正レンズが働いても、無限遠を目の遠点に映し出さなければなりません。鮮明な像が網膜上に映し出されるであろうことを確信させるために“光学”がそこから取って代わります。

　目が7Dの近視である時（“屈折異常”が角膜面にあると考えられる場合）、遠点は角膜から14.3cmに位置します。


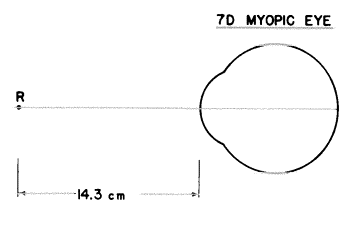
　“矯正”レンズは無限遠からの平行光線束を捕らえるために置かれ、レンズで屈折されたあと、それらがあたかもRから発せられているかのように目には見せるのです。そのようなレンズはその第2焦点F’がRと一致した時にだけそうなるでしょう。


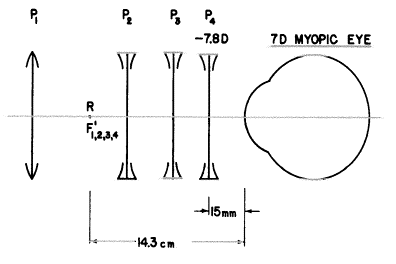
　それぞれがこの基準を満たした数枚の別々のレンズを下に示しました：

レンズ位置4は矯正レンズを角膜から15mmの“眼鏡面”に置きます。その屈折力は以下のようにならなくてはなりません：この7Dの近視眼では（再び角膜面での“屈折異常”です）、Rは角膜面から14.3cmにあります。レンズのF’は同じ位置になければならず、つまりレンズ位置4から(14.3−1.5)cmで12.8cmとなります。それでP4はとならなければなりません。P4の後ろにある目に無限遠からの平行光線をあたかもRから来たかのように見せるためにP4はその光線を発散させなくてはならないので、P4はマイナスにならなくてはなりません。


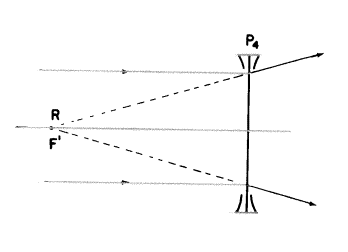
　もし矯正レンズが上の位置3に置かれたなら、それは必然的により短い第2焦点距離を持つことになりますので、P3はP4よりも大きなマイナスの屈折力になるでしょう。全ての可能な矯正レンズの中から、一番小さなマイナスの屈折力を持つレンズはRから最も遠くに位置することになり、つまり、角膜面に接した−7Dのコンタクトレンズがそうです。

　矯正レンズ2の位置がRからほんの1.0cmしか離れていないとしましょう。その屈折力はこの目を“矯正”するために途方もなく大きい−100Dにならなければならないでしょうが、その時無限遠の鮮明な像が網膜上に映し出されますので、確かにそれを光学的に矯正するでしょう。

　Rの左にあるレンズ位置1を今見てください。ここでもレンズはこの近視眼を矯正できますか？それはもちろんできます。しかしながらそれはプラスレンズでなければなりません。Rの左20cmに置かれたなら、この特別な“矯正”レンズは＋5Dの屈折力がなければなりません（そのF’をRに一致させて）―それは他の矯正レンズのように無限遠を遠点に映し出し、それによってこの7Dの近視眼で物体をきれいにはっきりと見ることができるのです。（この場合の1つの小さなポイント：このような方法で“矯正”された無限遠の物体の像は上下反対ですが、しかしそれにもかかわらず鮮明に見えるでしょう！）

 


 


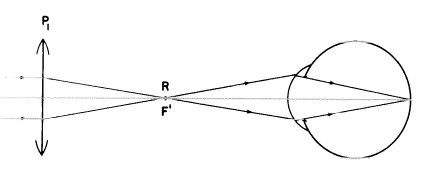
可能性として知っておくことを除いて、後者の常識的でない“矯正”を無視しましょう。

　通常の臨床的な立場で要約しますと：

　プラスレンズは遠視を矯正するために使用し、矯正レンズを目に近付けるほどその焦点距離は短くならなくてはなりません（プラスの屈折力が大きくなります）が、それはこれらのレンズの各々は遠視眼の後ろに位置した目の遠点とF’を正確に一致させなくてはならないからです。

　マイナスレンズは近視を矯正し、目にレンズを近付けるとその焦点距離は長くならなくてはなりませんが、それはRが目の前にあるからです。

　遠点がどこにあるのかあなたが知っている限り、近視や遠視の場合に適当なレンズをとても簡単に算出できます。

 

問題：

　3Dの近視を“矯正”するためには−8Dのレンズをどこに置けばいいでしょうか？

 

答え：


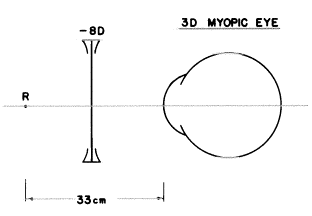
　3Dの近視眼は角膜の前33cmに遠点があります。

 

 


−8DのレンズはそのF’を、つまりそこから12.5cmに持っています。それゆえ、F’をRの上に重ねて置くには−8DのレンズはRから12.5cmになければなりません。これは目の前(33−12.5)cm、つまり20.5cmにレンズを置けばいいということです。

 

　頂間距離の変化で必要とされる矯正レンズ度数のこれからの交換や結合の全てをあなたは今把握できるのです。あなたが他の教科書で見つけるかもしれない公式に気をもまないで下さい。レンズの変化1mmごとに誘起される有効屈折力の変化がどれくらいなのかの数学的記述があれば十分です。しかしながら、あなたが知らなければならないのは1枚の“矯正”レンズの実際の屈折力だけです。この1枚のレンズは目の遠点であるRの位置を正確に示しますから、あなたが欲しいどんな頂間距離のどんな他のレンズでもあなたは決められるのです。“遠点”の美と屈折異常矯正に対するその臨床的な応用はみなさんに完全に明らかにされるべきです。