第３節　ナップの法則　（“臨床医のための光学”, p178-p180より引用）

　遠視眼の網膜像を作成してみましょう。でも眼軸がとても短いことが原因です（つまり、軸性屈折異常です）。私たちは同時にそのような3個の目を3個別々の網膜の位置で考えましょう。“異常”は屈折力ではなく長さにあるので、前部は3個の目全てに同じでしょう。

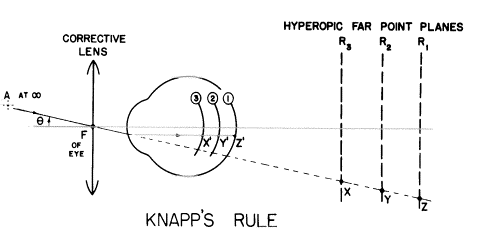
　各々の目はそれぞれに対応した遠点面を持つでしょう。目1はR₁に対応し、その他も同様です。私たちはこれらの目が同じ屈折力を持つと仮定しましたので、F（前焦点）はこれら全ての目で同じ位置です。

　もしこれら3個の目のどれでも点A（無限遠に位置する）を鮮明に見るなら、矯正レンズは対応する遠点面にそれを映し出す必要があります。レンズ自身の節点を目のFに一致させるために、適切な矯正レンズを前焦面に置きましょう。

　物点Aからレンズの節点で軸に交差するように光線を引きます。3個全ての矯正レンズでその光線は曲げられずに進むでしょう。目を越えて延長すると、この光線はAの像が映し出されるそれぞれに対応した遠点の位置を示します―それぞれX,Y,Zになります。（これら各々の面における像の実際の大きさは異なり、一番大きなものは一番遠くの面にあります）。しかし、この同じ光線は目のFを通過しますから目による屈折のあと（硝子体の中で）軸に平行になって出てきます。あなたは網膜の位置（軸性屈折異常の程度で変化するでしょう）はAの網膜像の絶対的な大きさに影響しないであろうことが分かります。像X’、Y’、Z’はそれぞれ黄斑部から全て同じ距離にあります。

　（前述の分析は軸性近視の前部にある近視の遠点面での近視矯正も網羅します。これはここでは図示しません。）

　ゆえに、非正視の程度もしくは方向（近視もしくは遠視）がどんなであっても、軸性屈折異常の中でFに置かれた適切な矯正レンズは事実上同じ大きさの網膜像を生じるでしょう。この網膜像は正視であるか否かにかかわらず、同一の屈折力を持つどんな目にある網膜像とも同じでしょう。これはナップの法則と言います。それが何か分かって下さい。でも臨床場面で使うには明かな困難があることを理解して下さい。あなたは存在する非正視が軸性なのかそうでないのかは決して分かりません（でも時々あなたは公平な考えがあるかもしれません―たとえば、単眼の高度近視の人の場合、非正視は軸性である可能性があります）。それで一般的に、私はとても明確に私の異端な意見を述べたいと思います。実用的な目的で、非正視が軸性なのか屈折性なのかに事実上の違いはありません。だから、ナップの法則は理論的にはそうなのですが、有用な応用はありません！