第3章 屈折異常
目がその見物人を十分に満足させようとすれば、鮮明な像を供給しなければなりません。これをするためにはさまざまな屈折面の力と目の長さの“適切で”調整された組み合わせがなければなりません。遠くにある物体の光の広がり(vergence)に完全に合った組み合わせが存在する時、私たちは正視が存在すると言います。もしそうではなくて組み合わせを誤ったなら屈折異常(非正視)が結果として生じます。
びっくりするのは、目の屈折力と目の長さがたびたび不適切に組み合わされることではありません。本当に不思議なのはなぜ不釣合いな組み合わせが偶然よりももっと頻度が低いかということです。もし母集団の中で屈折異常が存在している時に屈折異常の度数分布曲線を描くと、身長、体重、頭囲、その他のように“正規”分布ではないことに気が付くでしょう。正視(言いかえると、正視に近い―というのは実際の平均は約0.25Dだけ遠視側にあるからです)の度数が真に無作為な“正規”分布で予測されるものよりもすごく大きいのです。(グラフを見てください)
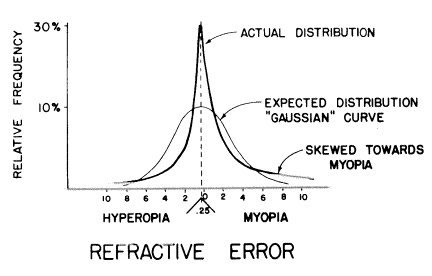
眼屈折の個々の構成要素である、角膜曲率、水晶体の屈折力、軸長(変性による伸長は無視します)が全て“正規”分布していることを学ぶとあなたは驚くかもしれません。“何か”がこれらの個々のパラメーターをたまたま調整しなければならず、その結果、眼球が大きくなりすぎた時には角膜の曲率半径も通常より大きくなる傾向があって、それゆえ屈折力が少なくなり、これで軸長の増加とつりあいをとります。反対に短い眼球は“正規”より尖った角膜と組み合わされる傾向があります。
だから、素晴らしいメカニズムが目を正視に近付けていることは明白でしょう。Arnold Sorsbyはこの傾向を“正視化過程”と呼んでいます。悲しいかな、時々それは失敗し非正視が登場します(そして、オプトメトリスト、眼科医、電気的屈折検査装置に仕事の機会を供給します)!
思い出すべき重要な点は(屈折異常がない)正視の眼球は大きな眼球でも小さな眼球でもいいということです。絶対的な大きさ(もしくはそれと相互に関係のある絶対的なジオプター度数)は重要ではありません―屈折力が存在している時にはその屈折力がその軸長に正確に対応している限り屈折異常は存在しないでしょう。ゆえに、小さい亀のちっぽけな眼球(たぶん6mmの長さ)と馬の眼球(たぶん60mmの長さ)の両方は正視のはずであり、それらの屈折の構成要素がそれらの軸長を完全に補償するのに十分強ければ鮮明な像が得られます。これらの例ではジオプター度数はそれぞれ270Dと23Dです。だから、あなたはジオプター度数を知るだけで非正視の度数もしくは方向を言うことは不可能です。あなたが知らなければならないのは軸長とそれに対応している屈折力がどのように相互に関連するのかということです。
“平均的”な人間の正視眼はおおよそ60D ですが、もちろんこれよりもまだ強いか弱い状態で正視かもしれません。私たちの目の光学的な図では正視の略式模型眼は60Dの屈折力で、n’=1.33(水の屈折率)の1つの中間透光体から構成されており、半径5.5mmのただ1つの屈折面だけがあります―これは本当の目からは歪められたモデルですが、便利です。
正視が存在する時、遠くの物体からの光線は鮮明な像が網膜に映るために焦点を網膜上に合わせるでしょう。つまり、1つ1つの物点は網膜面上に映るであろう像点によって表されます。眼軸に沿ってまっすぐ前に位置する遠点は、正視眼の網膜上にあるであろう第2焦点F’で像を結ぶでしょう。(下のAに示されているように):
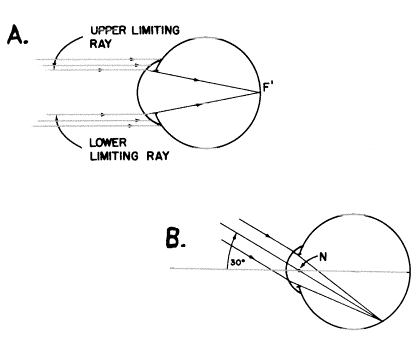
(上の両方の図では上と下のほとんどの光線は瞳孔の上端と下端をちょうどかろうじて通過していることを示しています。もっと周辺にあるどんな光線でも目には入れず、網膜像を形成するのには役立ちません。これらの中心から最も離れた2本の光線は“制限光線”と呼ばれます。軸の線は方向を決定するために示されています。)
上の図Bでは、もし無限遠の物体からの光線が軸外の点から発せられれば(軸の上の方へ30°とします)、目の節点を通る特定の光線は曲げられず、それゆえ像点の位置を決定するでしょう。その像は目が正視の時だけ網膜面にあるでしょう。(実はたとえどんな目の屈折力、もしくは屈折異常があろうとも像点はこの光線に沿ったどこかになければならないでしょう。それでこの光線がとても役に立つのです。)省略眼の節点は角膜前面から5.5mmのところにある曲率中心に正確に位置付けられなければならず、そして曲率中心を通るどんな光線もその曲面に垂直に突き当たらなければなりません―それでその面における入射角は0°であり―そして角膜前面によって曲げられることはありません。
角膜面と網膜の間の距離は、あなたがたまたま思い出さなければ簡単に計算できます。角膜面のPは60D、n’=1.33で、U+P=V
物体は無限遠なので、
U=0
像の距離 v=f’(第2焦点距離)
ゆえにF’ (正視眼では網膜上にあります)は角膜面から22.2mmのところにあります。
もし目が正視でなかったら、それは屈折力が強過ぎるか弱過ぎるか、もしくは軸長が長過ぎるか短過ぎるかのどちらかです。“過ぎる”というのは相対的な言葉で、それは目を“矯正”するためには何が必要なのかに言及するだけです。存在する非正視の度数を表現しようとする時はいつもその目の正視からどれくらいの屈折力の差で“離れている”のかを示すだけでよいのです―“正常”や“平均”の屈折力、他の任意の標準からの差ではありません。