第１０章 曲面屈折
さあここで曲面が光線に対しどのように振る舞うのかを調べてみましょう。
お願い：この1つの誘導があなたを恐怖に追いやってしまうのは本意ではありません。私の言うことを我慢して聞いて、最後までやり通す努力をして下さい。それはいくつかの数学記号の使用にもかかわらず難しいことではありません。実はあなたの有用な公式である、U＋P＝Vがどのようにして導かれたかを正確に学ぶのは面白いことだと分かるかもしれません。しかしながら、簡単な数学でさえ嫌気がさすという読者はややこしい数式は跳ばしてp.61に進んでも結構です。
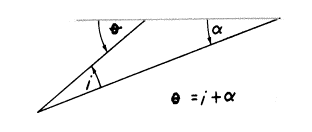
曲面でなにが起こっているのか見るには、2つの点があなたの幾何学の素養から復活されなければなりません：
a) 三角形のいずれかの外角はその反対側の2つの内角の和に等しい：
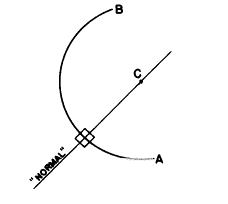
b) 球面に対して（垂直な）“法線”は曲率中心を通るいずれかの直線です。もしCが円弧ABの中心であれば、示された直線はその面に対する“法線”と考えられます：
それでは、曲面における屈折をちょっと見てみましょう。入射光線1が中心がCである球面上の点Pに突き当たります。（次の図を見て下さい。）
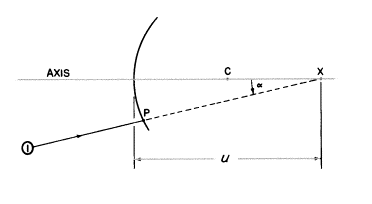
もしこの光線が面に当たらなければ、光は進み続け軸を点Xで横切ります。（光軸に沿って測られた）Xまでの距離は物体距離u、そしてこの光線1の軸に対する角度はαとします。
点Cから点Pまで直線を引きます。これは面に対する“法線”です。“法線”は点Cで角θを作り、入射光線1はこの“法線”と角iを作ります。角iは“入射角”で、それはその（2本の交わった線で作られる）対頂角と等しく、三角形PCXの1つの角として下に示されています。
θが△PCXの外角であるから、
θ＝α＋i
ゆえに、 i＝θ−α
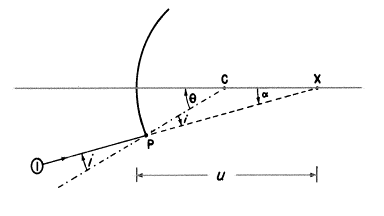
光線1は面によって屈折させられて“法線”の方向に曲げられるでしょうし、“屈折角”は今i’とします（次の図のとおり）。
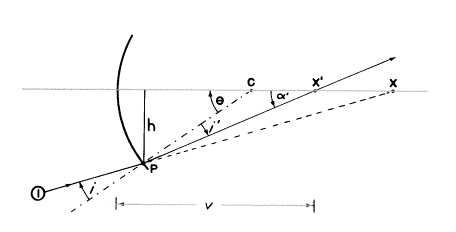
この屈折させられた光線は進み続け、球面から像の距離vで軸に点X’で交わり、軸と角α’を作るでしょう。
θは△PCX’の外角でもあるので、つまり、
θ＝i’＋α’
そして、 i’＝θ−α’
それで、私たちは次のように表しました。
i＝θ−α
i’＝θ−α’
小さい角度では私たちはスネルの法則を簡単にして、
ni＝n’i’
ゆえに、iとi’に代入すると、
ni＝n（θ−α）＝n’i’＝n’（θ−α’）
私たちは次のように導くことができるでしょう。公式1：
n（θ−α）＝n’（θ−α’）
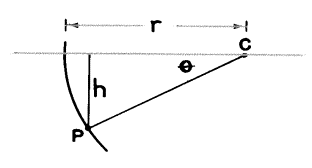
点Cから曲面までの距離はもちろんその面の半径rです。点Pが軸から距離hのところにあると仮定しましょう。点Pが比較的接近している時、つまり、hが短い時、θは小さな角になり、そしてhはθに対して張っている円弧の長さにほぼ等しくなるでしょう。だから、ラジアンでは、
θ＝
これまでの図から同じ理由を使って、あなたは次のことが分かります。
α’＝
そして α＝
実際の角それ自身（θ、α’、そしてα）を考えることはやめて、公式1の中の角にそれと等しい表現を代入します。
n（θ−α）＝n’（θ−α’）
hを括弧の外に出すと、
hで割ると、
これを展開すると
整理すると
だから
もしくは
やった！これは単一球面の屈折に関する一般的な関係です。それは物体の光の広がり(object
vergence)（
）、像の光の広がり（image vergence)（
）、そして面の屈折力(
)を結びつけます。なにかよく知っているものに見え始めませんか？次のようになります！
P [1]
U＋P＝V
私たちの薄い単レンズとそれらの屈折力(vergence power)について話す時、レンズの両側にある媒質の屈折率は同じで、nとn’は1.0に等しかったのです。しかし、もし媒質が空気でなかったら、物体の光の広がり（object vergence)と像の光の広がり（image vergence)に屈折率が影響し、Uは
と等しくなくなって
と等しくなり、Vは
と等しくなくなって
と等しくなるので、私たちは屈折率を考慮しなければなりません。
初めに私たちはレンズPの屈折力は適当なジオプターの数値で考えましたが、今度はそのようなレンズの全体的なレンズの屈折力はその2つの面屈折力に左右され、それぞれは順番にそれぞれ自身の曲率半径と屈折率の違いによって決まることを見てみましょう。薄いレンズでは2つの面のそれぞれの屈折力を単純に代数的に加えあわせれば十分です。前面の＋5Dと後面の＋3Dは合計して全体の屈折力である＋8Dになります。同様に前面＋7Dと後面−1Dは全体の屈折力として＋6Dを生じます。（後者のレンズはメニスカスの形という点でたいていの眼科の矯正レンズと同様であり、つまり、それは目に対して凹面になっています。）だから、一般的にPtotal ＝P1＋P２です。これは薄いレンズのためのものです。しかしながら、厚いレンズでは、真の“等価”レンズ屈折力にするために、面屈折力の合計から引かなくてはならない3番目の厚みの要素[
（P1）（P2）]があります。あなたはこのコースでは厚いレンズは扱わないでしょう。
ほんの２、３の公式を覚えなければならないと私が言ったことをあなたは思い出せますか？そう、それらのうちのもう1つがあります：
はどんな面の屈折力にもなります。よく覚えておいて下さい。それは、rが小さい時には曲面屈折力は高くなります。もしrが大きければ屈折力は低くなり、もし無限に大きければ屈折力はゼロになるということです―平面がちょうどそのような面であり、屈折力(vergence power)はゼロです。
問題：
a) 半径10cmであるガラス棒（n＝1.5）の磨かれた凸面の屈折力は空気中ではいくらですか？
b) 同じガラス棒が水（n＝1.33）につけられたあとその屈折力には何が起こりますか？
答え：
a) P＝
P＝＋5ジオプター
b) P＝
P＝＋1.7ジオプター。つまり、水につけることによりガラス棒の屈折力が減らされたのです。
薄いレンズについて言えば、P＝
；
単一面もまた焦点距離があり、上式と同様にそれらの距離を決定するには屈折力に対する逆数の関係を使うことができますが、物体と像の空間の屈折率を考慮しなければなりません。
Psurface＝
これが意味するのは、空気と水の境界面が＋5ジオプターの面屈折力を持つなら、空気中でのfは
、つまり、＋20cmとなりますが、水の中ではf’（無限遠に位置する物体の鮮明な焦点の位置）＝
＝26.5cmであり、面の右にできるということです。
これは面の片側の媒質が空気であれば高密度の媒質中にある第2焦点は第1焦点のn’倍、f’＝n’fとなり、利用しやすい関係であることが分かるでしょう。
要約：レンズと面屈折力を扱うどんな計算でも物体と像の光の広がり（object and image
vergence)は参照する面からの実際の距離だけでなく、物体と像の空間の屈折率に左右されることを忘れてはなりません。私たちは模型眼を学ぶ時にこれらの概念についてもっと探求するでしょう。
問題：
物点Xは水のタンクの中に置かれ、タンクの端から40cmの距離にあり、タンクの端は半径5cmの凹面になっています。空気がタンクを包み込んでいます。
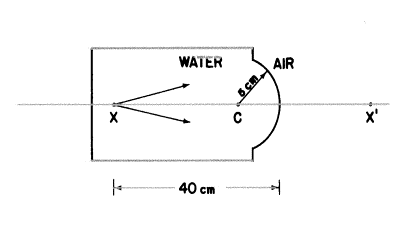
a) どこに像点は結ばれるでしょうか？
b) 屈折面の第1と第2焦点距離はどれだけでしょうか？
答え：
a) U＋P＝V
U： 光線はXから曲面に突き当たるように発散していき、ゆえに、光の広がり（vergence)は面においてマイナスです。
物体空間の屈折率は水の屈折率であり、1.33です。ゆえに、物体の光の広がり（object vergence)である
。
P： 
における屈折率の差はいつも像空間の屈折率から物体空間の屈折率を引いたものです:ここでは、（nair−nwater）＝1.0−1.33＝−0.33です。r＝5cm＝（0.05m）ですが、ただ左から右へ入射してくる光に対して凹面ですので、マイナスになります。r＝−0.05mです。
だから、
となります。
（ゆえに、像空間の屈折率が物体空間の屈折率より小さい時、私たちは凹面はプラスの屈折力を持つことが分かります。）
V： 像光線の光の広がり（vergence)＝
であり、n’はここでは像空間の屈折率であり空気ですからn’＝1.0となり、V＝
です。
それでは、Vに関する方程式を解くと：
U＋P＝V
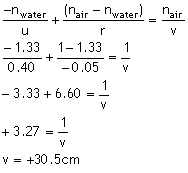
Xの鮮明な像がX’、屈折面（水タンク側面）の右側30.5cmのところにできるでしょう。
b) 第1焦点距離＝
f＝＋20cm（水の中）
第2焦点距離＝
f’＝15.1cm（空気の中）
（両方は球面の軸上頂点から測られます。）
（横倍率に関する物体と像の空間の屈折率の影響についての議論は付録Aを見てください。）