第３節　マイナスレンズ

　マイナスレンズは入射光線に対して発散を加える能力を持っています。同様なU＋P＝Vというわずかな関係と、私たちが関係した全ての符号の慣習は生き続けています。

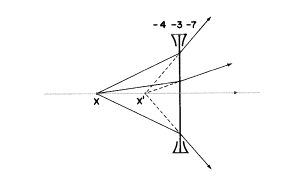
　−3DのレンズPの左25cmに実在する物点Xが位置していたら、レンズにおける物体の光の広がり（object vergence)は、つまり−4Dとなります。−3Dのレンズは−4Dで入射する光の広がり（vergence)に、その−3Dの屈折力(vergence power)を加え、像の光の広がり（image vergence)である−7Dを生み出します。

　　　　　　　　　　　　U＋P＝V

　　　　　　　　　　　−4＋(−3)＝−7

これは像点を、つまり−14.1cmのところに位置させ、マイナス符号は再び“レンズPの左側”を意味します。

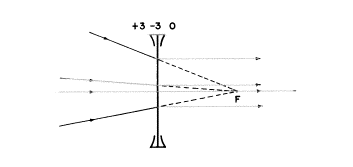
　もし、物体（次の図に示す）が左無限遠にあったら、物体の光の広がり（object vergence)Uはゼロになるでしょう。

　　　　　　　　　　　U＋P＝V

　つまり、0＋(−3)＝−3

よって、像の光の広がり（image vergence)は−3ジオプターであり、像点は−33cm（レンズPの左33cm）のところにあります。私たちはすでに無限遠上にある軸上の物点と共役関係にある像点はレンズの第2焦点F’と呼んでおり、だからこのマイナスレンズのF’は左33cmにあります。

どのマイナスレンズでもF’はいつも左にあるでしょう。しかし、プラスレンズのF’と同様にF’もまたまだ像であることを忘れないでください。無限遠上の物点は、それがたとえレンズのF’と同じ側にあるように見えても、それは同じ“空間” ではありません。像点F’はただ“像”空間にのみ存在するのであり、その言葉は与えられたレンズによってすでに影響された光を私たちが扱っていることを意味しているのです。

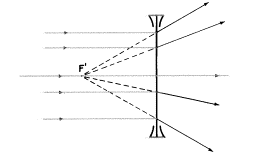
ここで、定義によりマイナスレンズの第１焦点（F）は物体であり、その像は右無限遠上になければならないので（つまり、像の光の広がり（image vergence)はゼロでなくてはならない）、いったいぜんたい私たちはどのようにして（F）を位置付ければいいのでしょうか？私たちの信頼できる関係U＋P＝Vは私たちを助けてくれるでしょう：

　　　　　　　　　　U−3＝0

U＝＋3でなければならず、その意味するところはこの物点F（レンズの第1焦点）はレンズの右33cmになければなりません。私たちの光線（この慣習を覚えていますか？）は左から右へ進まなくてはなりません。だから、私たちにとってゼロの像の光の広がり（image vergence)を得るためには、物体の光の広がり（object vergence)は物体空間でプラス（収束）でなければならないのです。ただその時のみ平行光線がマイナスレンズによって作られます。（この論文の中で先に述べたように、収束する物体の光線は他の光学的装置によってのみ形作られ、それらは自然には発生しません。）

図でマイナスレンズのFを説明するために、物体の光線がレンズに突き当たる前にF（“物”点）に向かって収束することを私たちは示さねばなりません。物体の光線が決して実際にFに到達せず、ただそこに向かっているという事実はあなたを苦悩させることはないでしょう。

収束光線が任意のレンズ―プラスもしくはマイナス―に向かう時、物体の光の広がり（object vergence)はもちろんプラスでしょうし、そして触れることができないので、物体は“虚(virtual)”と考えられます。しかしながら、光学的には虚の物体は虚像と同様、実在する物体と同じように容易に扱われます。虚の物体光線は次にありますように実線のかわりに点線にして図に示してあります。

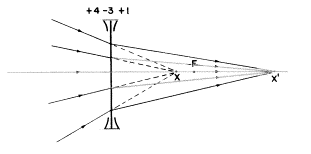
ここで虚の“物体”をレンズに近付け、レンズとFの間のどこかに持っていきましょう。そうすると私たちは物体の光線を＋3D以上に収束させなけなければならないでしょう。もし物点Xの光の広がり（vergence)が＋4ジオプターだとすると（下図を見てください）

　　　　　　　　　　 　　U＋P＝V

　　　　　　　　　　 ＋4＋(−3)＝＋1Dとなり、実像点がマイナスのレンズによって作られるでしょう。もしあなたが望むなら、この像を右の1m先にあるスクリーンに映し出すことができます。