第２節 プラスレンズ
ここでレンズ―どんなレンズでもかまいません―を私たちの光を発する点Xの右側のどこかに、そうですね、66cmのところに置いてみましょう。点Xからの光の広がり(vergence)はレンズ面で測ると−1.5D（レンズがそこになかったとしてもその位置での光の広がり(vergence)は同じになります）です。レンズはレンズに入射する光の広がり(vergence)を変えるある特性があります。光の広がり(vergence)を変える能力はジオプターでも表現されます。レンズは入射光に光の広がり（vergence)を加えるのであればプラス（＋）と考え、光の広がり(vergence)を減じるのであれば（つまり、光がもっと発散します）マイナス（−）になります。
点Xの右50cmのところに＋3Dのレンズを置くと、レンズ面のところで−2Dの光の広がり(vergence)をすでに持っている入射光に＋3Dの光の広がり(vergence)をレンズは加えるでしょう。光線は＋1Dの光の広がり(vergence)を残すでしょう（もう一度いうと、レンズ面で測った時です）。下の図を見てください：
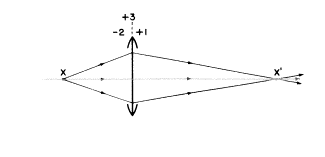
レンズ面で生じる光の広がり（vergence)の計測に注意し続けるために、入射光がレンズに当たった時、図上でレンズのちょうど左のところに−2を書きます。これは物点Xの光の広がり（vergence)であり、U（ジオプター）と呼びましょう。屈折力Pの値である＋3Dは物体の光の広がり（object vergence)と一緒になって（に加えられ）、結像点での光の広がり（vergence)V、となり、レンズのすぐ右に＋1ジオプターと書かれます（もう一度レンズは参照面であることを思い出させるために）。私たちが言ったことは数学的に略して書けます。
U＋P＝V
物体の光の広がり（object vergence)はレンズによって供給される光の広がりを変化させる力（vergence-change)と組み合わされ、像の光の広がり（image vergence)を生みます。これはあなたが知らなければならない数少ない鍵となる“公式”の1つです。私たちはそれに強く信頼を持ち続けるでしょう。
再び慣習で、光の広がり（vergence)は大文字で表されます：物体はU、像はVであり、そして小文字のuとvはそれぞれ物体と像の距離に対応します：
先の物体−像の例は収束、つまり＋光線に対する私たちの初めての出会いです（ここでは像に関して）。私たちはそれらを作るために光学的なシステムを使うことが分かります。“＋1D”の像の光の広がり（image vergence)はレンズPから出る光線が収束し（＋符号）、レンズPの右
に位置する像点に向かっていくのです。ジオプターでいう像の光の広がり（image vergence)は＋1Dと分かっているので、像点までの実際の距離は
になります。ゆえに、点X’（物点Xに光学的に対応する像点）はレンズPの右1mに位置します。像点は実在するもので、スクリーンに焦点を結びます。
XとX’は共役点と言われています。それらはお互いの物体と像を位置させることで関係しています。光線は完全に元にたどることができるので、実在の物点をX’に代わりに確実に置くと、レンズPによるその像はいつもXのところに正確にできます。しかしながら、（私たちの慣習で）右から左に進む光は使用しないことに同意しています。でも、それらはそのようにできることを理解してください。（鏡はこれらの光線の方向を逆転させるでしょうが、これはあとで探ります）。
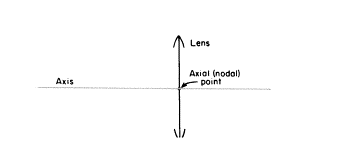
もう1つの定義を整理します。レンズの軸：この線はレンズ面に垂直に入る光線と一致し、表現するもので、また、その光の進行方向はレンズによって妨げられず、軸上の光線は曲がらずに通り過ぎます。
この光線が当たるレンズ上の点は軸上点(axial point)です―私たちの全ての光学的な構造のために決定的なものです。実は軸上点を通過する全ての方向からのどの光線も曲がらずに進みます。私たちはこの点を節点(nodal point)とも呼びます。ここでの“薄い”レンズシステムに関しては軸上点と節点は正確に一致します。私たちがより複雑な光学システムを勉強する時はそのような点をもっと調べるでしょう。
思い出してください。私たちは多くの点から構成されるかなり大きい物体の中の一点を意味するXを選びました。与えられた光学的な例の中で私たちのレンズPから等しい距離にあるどのXも私たちは選ぶことができました。つまり、物体の全てのそのような点はレンズの軸と垂直でレンズPに平行な面にあるに違いありません。これらの点は物体面を構成しています。（同じ物体上の他の点ではあっても同じ面になければ必然的にレンズのところで違う光の広がり(vergence)を生み出します。）
ちょうどXが物体面を形作ったように、X’（Xの像点）もレンズPに平行な像面を決定します。Xと同じ物体面の中にある全ての点は、X’と同じ像面のどこかに像を結びます。これらの点に対応する正確な位置はあとで決定されるでしょう。
私たちの同様な＋3DのレンズPについて振り返ってみますが、物体Xをレンズにもっと近付けてみましょう。Xがレンズから50cmから40cmまで動いた時、そのレンズのところでの光の広がり（vergence)は−2から−2.5ジオプターまで増えます。
U＋P＝V は −2.5＋3.0＝＋0.5 になります
その像線はまだ収束していますが、レンズから新しい像であるX’までの距離は今増加しました。X’はもっと右へ移動し、
、つまり2m離れた位置になっています。
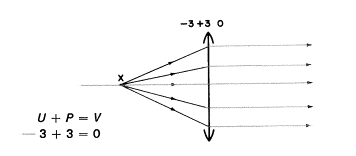
Xがもっと近付いていくと―33cmまで近付くと―少し奇妙なことが起こります：
U＋P＝V
−3＋3＝0
像点での光の広がり（vergence)はゼロとなります。レンズPからの距離はvです。
v＝
“なんじはゼロで割られることはない”という数学上の戒律がありますが、ここではV＝0ですからいったいどうなるのでしょう？私たちは物点Xに対応する像点はないということは言えませんが、言えることは像の光の広がり（image vergence)Vはゼロに近付くので、vは右へ向かった無限の距離に近付きます。つまり、像点X’は遠く離れたところ、“右の無限遠上”に位置します。
ここで私たちはレンズPに関係した物点Xの特別な位置を発見しました―この物点の位置は、像点が無限です。レンズの軸上のその位置はレンズ第1焦点(primary focal point)（F）と呼ばれます。そこで生じレンズに当たった光線は平行の束となってレンズから出ていきます。
Fを含むその面（レンズ面に平行）は第１焦面(primary focal
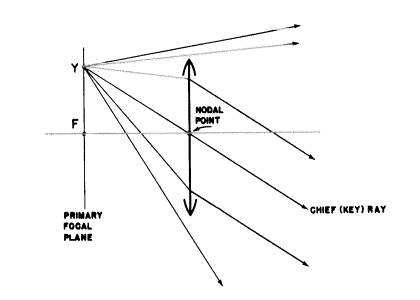
plane)です。この面のどの位置にあるYでももちろん発散する光線を射出します―レンズPに降り注ぐそれらの光線はお互いに平行に“像空間”（レンズの働きによって）に入ります。でも、どの方向に平行なのでしょうか？確かにレンズの軸に平行ではありません。というのは軸上点Fそれ自身のところで明確に生じる光線だけがそうなるからです。そうです、像の中にあるこれらの平行な光線によって生じる方向は物点Yから射出される光線のただ1つだけによって示されるでしょう―Yから射出されるその特別な光線はレンズPの軸上（節）点に向かうのです（下の図を見てください）。つまりその光線は（私たちの節点の定義によれば）曲がらずに進み、第1焦面にある点Yで生じる“像空間”における全ての平行光線の方向を決定します。
私たちは今レンズの焦点距離（つまり、Fとレンズの間の軸上の距離）は、この特別なレンズPで像の光の広がり（image vergence)がゼロになる明確な物体の距離u以外の何物でもないことが分かります。だからメートル法でいうfは
に違いありません。
それで、私たちの次の簡単な“公式”は
f＝
＋14Ｄのレンズは
、つまり＋7.1cmの焦点距離になるでしょう。
もし私たちが映写機のレンズの第1焦面の位置に35mmのスライドを置き、その上へ強い映写機の電球を光らせることでスライドをとても明るくすれば、レンズはスライドの像をスクリーンの上に大きく映すでしょう。もしスクリーンが右の無限遠上にあればその像は鮮明で明確でしょう。それはかなり長い映写室のためのものですから、スライドはFに少し達しないようにして、つまり、レンズから少し遠いところに置くようにします（そうすると、スライド上のそれぞれの点から射出される光線の広がりはいくらか減少します）。それで、拡大された像はレンズのまえにある有限の距離上で発見できます―ほとんどの映写機のためには無限遠より少し実用的です！
いままでのところでは私たちは軸上の物点Xをレンズに近付けた時像点はどのように動くかを見てきました。ちょっと振り返ってみましょう。軸上点Xがレンズの左の離れたところ（左の無限遠上）にある時、それから発せられる光線は自然に発散します。しかし、レンズはとても遠いところにあるので、光線はレンズに届くまでにあまりにもわずかしか発散しないことにより、私たちは光線を平行な束で到達すると考えなくてはならず、それはゼロである物体の光の広がり（object vergence)Uとなります。
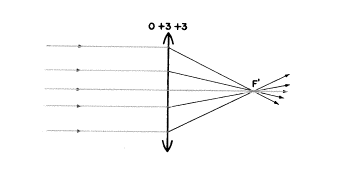
下の図にあるレンズを見ますと、何本かの平行光線が引かれていますが、それらの全てはレンズ左の無限遠の軸上に位置する1つの点Xから来ていることを思い出してください。
軸上の物点Xの像はF’で、第2焦点(secondary focal
point)（もう1つの鍵となる位置）となるでしょう。F’は無限遠上に位置する軸上の物点に対応する（共役である）像です。
＊ ＊ ＊
驚いたことに、初心者によってたびたび描かれる典型的な誤った図があります。しかし、不幸なことに、簡単な光学が“説明されて”いる時、初歩の物理学や生理学の教科書でもそれは時々見つけられます。私はそれ、つまりそれの手頃な複写を見るたびに震えてしまいます。今はあなたもそうでしょう！
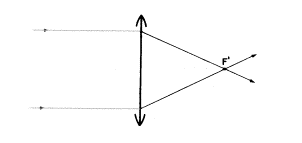
下図は正しいものです。
引かれた2本の光線は、焦点F’に進んだ時、とても遠くにある物体の1点（軸上点）から発せられた光をもちろん示しています。
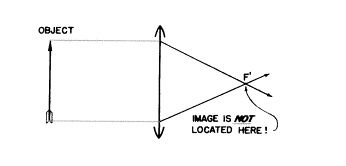
では、この図を見てみましょう：
矢の形をした物体のそれぞれの端から1本の光線が描かれたこの図は、私が信じるに、実は同じことを示そうと試みています（つまり、焦点F’における最終的な像です）。しかし、この図はひどく間違っています。矢の本当の像はF’よりもっと右にできるに違いありません。このような図やその同類はなにか簡単なものを理解できる自信をうち砕くことによって、学生を混乱させることに終始しています。あなたはこの同じ間違いをしていませんか。もうこれ以上言うことはありません。