第１節　回旋倍率(Rotational Magnification)

　レンズを通して軸外の物体を見上げるにはどれくらい目の回旋が必要なのかを見て、この回旋を同じ物体をレンズなしで見るのに必要な回旋と比較してみましょう。この比較は百分率が使われるので拡大として見られる可能性もあります―だから横倍率、角倍率、そして縦倍率に加え、回旋倍率もあるのです。このタイプは他と関連性はなく、重要な考えではありません。実際は（生じる徴候を中心に話せば）患者にとって眼鏡レンズの角倍率と同じくらいかそれ以上に重要かもしれません。

　下の図を見て下さい。

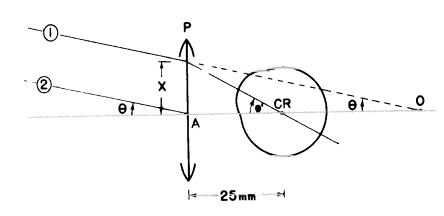
目は角膜が約15mm離れるように矯正レンズの後ろに典型的に置かれます。目の回旋点CRはおおよそ目の“中心”に当たり、角膜からたぶん12mm後ろになります。だから回旋点はおおよそレンズの後方25mmになります。（2mmの違いにけちをつけてはいけません。それを無視すると算数が簡単になります！）

　無限遠の物体からの光線1はレンズ（ここではプラスレンズです）に突き当たります。この光線は屈折の後目の回旋点で軸と交わるように選ばれました。それが軸と作る角はθ’です。これはレンズを通して無限遠の軸外物体を見るために目が回旋しなければならない角です。レンズなしではこの目は同じ物体を見るためには角θだけ回旋しなければならないだけです（ここではθはレンズの節点を通る光線2で表されています。）

　光線1は光線2と平行です。だから、もし私たちが光線1を進め続けるなら（レンズを通過しますが、それによる屈折はありません）、それも角θで軸を横切るでしょう。光線1のこの直進は点Oで軸と交わるでしょう。

　しばらくの間、無限遠にある1つの物点から光線1と2両方が生じる事実を無視して、光線1を見ましょう。それと軸は2本の光線を表すことができ、両方はOに向かっています。その時、それらは共にレンズの虚の物点として点Oの位置を固定しますから、回旋点は対応する像点となることが分かるでしょう。ゆえに、軸上点Oと回旋点は共役であり、レンズからOまでの距離は距離uとなり、レンズから回旋点までの距離(ここでは25mm)はvです。

　　　　　　U＋P＝V；　またV＝

　ゆえに、　　　U＝40−P

　　　　　　　 u＝；　またv＝

　微小な角において示されているレンズ面の長さxでは、

　　　　　　

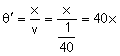
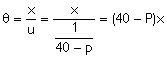
回旋倍率＝

　M_rotational＝

　この関係は眼鏡レンズ面に位置するどんな矯正レンズ（プラスもしくはマイナス）でも真です。無水晶体眼用レンズの＋12Dでは回旋倍率は

　　　　　　　　つまり、143%

ゆえに、無水晶体眼はその矯正レンズを通じて、同じ物体を見ている無水晶体眼でない目よりも43%大きな回旋を働かさなければならないのです。すでに記述したように、患者の外直筋に加わる緊張は彼の網膜像が25%の角倍率になるよりももっと大きな問題を提示するかもしれません！