第7章 スネルの法則と屈折率
私たちのコースの“重要な部分”である、目の光学―私たちが本当に待ち望んでいた課題―に夢中になれる前に、私たちはもう2、3の熟知した原理が必要です。この現在の章はやむを得ず少し数学的ですが、確かにそんなに不快ではないので、偏見を持たずにそれに近付いてください。
最初に私たちは光の広がり(vergence)と、レンズがその光の広がり(vergence)を変える方法の概念に取り組むことで始めたのですが、私たちはレンズが本当にどのように働き、何がその行為を支配しているのかという背景をあなたに与えることを怠りました。初めに取り組むといいことは、全てのレンズと屈折面に像を作るために働かせる光学の基礎的で基本的な法則、スネルの法則です。
この法則で屈折率が違う媒質によって分けられている表面でそれぞれの光線がどれくらい曲げられるか正確に分かります。あなたが早くに学んだ物理学のコースから、この屈折率は透明な媒質の特性であり、光線が真空以外の媒質を通り過ぎる時には遅くなることを思い出してください。屈折率は特定の媒質中での光のスピードと比較して、真空中で光がどれくらい速いかという比率です。屈折率は
![]()
分数の分母はいつも分子よりも小さいので、この比率nは真空(実用的には空気)以外のどんな媒質でも1よりいつも大きくなります。
おもしろいことにどんな媒質の中でも光の進む速度は媒質自身だけでなく、光そのものの波長にも依存します。各々の波長にはそれ自身の“独自の”屈折率がそれぞれの媒質に対して存在し、あなたが通常見る表の中に並べられている屈折率はナトリウム光線の特別な波長である589nm(10−9m)における場合です。水の屈折率はn=1.333、眼鏡のクラウンガラス(1.523)、プラスチック(1.491)、水晶体(1.42)、角膜(1.376)です。
1つの媒質を進んでいる光線がより強い屈折率の他の媒質に入射する時、その光線は遅くなるでしょう(反対も同様)。もしそれが物質の表面に垂直(“法線”)に入射するなら、それはやはり遅くなるけれども、方向は変えずに表面に対して90゜の同じ方向に進み続けます。しかしながら、もし光線が新しい媒質に“法線(normal)”に対していくらかの角度(傾き)で入射するなら、それは境界に交わったあとで曲げられるでしょう。スネルの法則はこの光線がどれくらい曲げられるのかを教えてくれます。
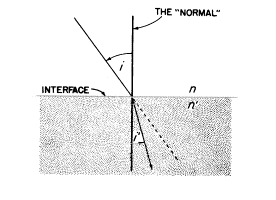
境界面(interface)の一方の側にある媒体の屈折率をnとし、相対する側をn’としますが、これらは光線の単一波長で示されていることを思い出してください。入射光線が“法線”との間に作る角度を私たちはiと呼びます。新しい媒質に入ったあと、光線は曲げられます―もしn’がnより大きければ法線のほうに向かいます。屈折のあとの角度はi’によって示されます。iとi’はそれぞれ入射角、屈折角と呼ばれ、光線が当たったところの点における面に対して垂直に引かれた線である、“法線”に対していつも測られます。
スネルの基本法則―全ての屈折を支配し、レンズが光線の方向を変えるに当たってどのように働くかの基本を形成―は次の通りです:
n sin i=n’ sin i’
十分に簡単です。しかし、これは三角法の関係を表しているので、もっとそれを簡単にしてみましょう。(あなたは理解すべき単位に無意識に精通するでしょうから、私はこれを完全に経験することが明らかに時間をかけるだけの価値があると感じます。)