第５節　天体望遠鏡

　ガリレイ式望遠鏡とその操作原理は眼光学と屈折異常の矯正に密接に関係しています。しかし、角倍率を供給する無焦点システムはこの道具だけではありません。もう1つ“天体望遠鏡”と呼ばれるとても有用なものがあり、それは像を拡大しますが倒立像になるのです。もしそうでなければその光学はガリレイシステムのものにとても似ています。

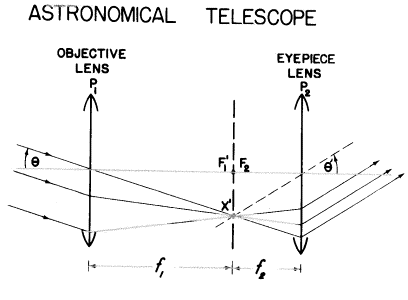
　この拡大装置前面の（対物）プラスレンズP₁はちょうどガリレイシステムと同じように第2焦面（F₁’）に無限遠上の物体の実像を作ります。しかし、ここでは第2のレンズP₂（接眼レンズと呼ばれます）はプラスです。それはその第1焦面F₂が対物レンズのF₁’面と一致するように置かれます。P₁によって作られた像点X’は今P₂の物点のように振舞うでしょう。X’がP₂の第1焦面なので、その最終的な像は無限遠になるでしょう。ガリレイ式望遠鏡のように、光線の最終的な平行光線束が軸との間に作り出す方向（角θ’）は節点P₂（それは軸上の頂点）を通ってX’から引かれた線で与えられます。P₁の節点ではθは物体角になります。

　この望遠鏡の角倍率はです。しかし、図からも分かるようにθ’とθは反対方向です。角θで示された物体は軸の上であり、一方角θ’は対応する像X’が軸の下に位置していることを示します―これは物体と像の両方とも同じ方向にあったガリレイシステムと対照的です。だから、M＝です。

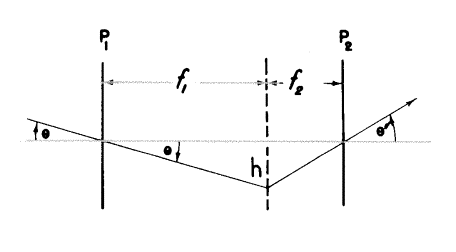
上図を簡単にするために（まだ微小な角を考えています）、下図を見てみます：

　　θ＝

　　θ’＝

　　θ’はここでは時計と反対方向ですから、

　　M＝

これはガリレイ式望遠鏡の倍率ですでに与えられたのと同じ表現であることに注意してください！ゆえに、どんな望遠鏡でも倍率はの関係によって単純に与えられます。

　これから、屈折力の割合が一定になるどんなレンズの組み合わせによっても同じ倍率が供給されうる可能性があることが明らかでしょう。3×の望遠鏡は＋9DのP₂と＋3DのP₁、もしくは＋21DのP₂と＋7DのP₁から構成されてもよいのです。（レンズ間の距離は必然的に後者の組み合わせでより短くなるでしょう。）

　天体望遠鏡の原理は倒像鏡(indirect ophthalmoscope)に臨床場面で利用されています。この同様な原理（実際の物体をP₁に非常に近付けるためにいくらか修正されています）は標準的な光学顕微鏡の基礎です。