第１節　光の広がり（vergence)

　色とりどりの花瓶、白黒写真、棒、スネレン試視力表の文字Eなど、どんな物体でも無数の点から構成されていて、それぞれの点は物体の全ての組織に何か寄与しています。物体の像を形作るためには物体から出てくる光が必要です。光は強くなくともよく、実際はごく弱いものでよいのですが、ある程度は必要です。光のエネルギーは物体によって発せられ、物体から反射され、物体を通して伝えられますが、なんとかして光のエネルギー（それは目にさえ見えないかもしれません）は発散されなければなりません。つまり、物体は“発光”するものと考えられるのです。物体から多くの光線が発せられますが、それぞれは無限に薄く、特定の方向に発せられるのです。

　私たちは光線を知能でもって扱えるまえに、光線のある性質に同意しなければなりません。これらは光の慣習に関係があり、これらの“動物”を扱うための単なる私たちの規則なのです。慣習の1つに光は左から右に進むということがあります。もちろん光は全ての方向に進むのですが、ここでの分析では光線の最初の慣習に同意していただきたいのです。

　光線は実在する物体を構成している全ての点からいつも発散していく（別々に広がっていく）ので、ここで物体上の任意の１点Xから発せられる光線に焦点をあててみましょう。

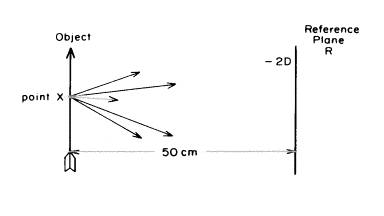
　上図には点Xから発せられる多くの光線の中から5本の光線が引かれており、右へ進んでいます。これらの光線は、そうですね、50cm離れた参照面に到達しています。光線がこの平面に到達した時光線はある比率で発散しているのです。私たちは参照面で点Xから発せられた光線の光の広がり(vergence)は、点Xと平面の距離に反比例していると定義（説明ではなく）します。つまり、参照面Rでは点Xから発せられた光線は＝2ジオプターです。私たちの慣習で再びいうと、全ての参照面において発散している全ての光線は負（−）であると考えますので、ここでの実際の光の広がり（vergence)は−2ジオプターのように記載されます。

　全ての実在する点からの全ての光線は発散します。収束する光線をあなたが横切ったら、それらは他のなんらかの光学システムによって作られていることを理解していただきたいのです。というのは収束光線は自然には起こり得ないからです。これらは慣習で正（＋）と定義されます。この本ではこの符号の慣習を終始用いています。しかし、このことを確かめるために他の教科書を調べないでください。教科書によってはこの慣習を使っていないこともあるのであなたは混乱してしまうでしょう。この本の方法で学んでいただきたいのです。もう一度言いますが、レンズ、鏡、目、光学システム、どの場合についても、マイナスは発散光線であり、プラスは収束光線を意味します。簡単なことです。

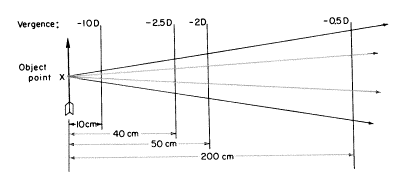
　もし参照面を点Xに近付けほんの40cmの距離になったらその時の面における光の広がり（vergence)は−2.5ジオプターとなります（）。 10cmでは−10Dであり、2mでは−0.5Dとなります。マイナス符号を忘れてはいけません。

　もし完全に実際の面をなくせば点Xから規定の距離における光線の広がり方についてまだ話すことができます。この広がり方は光線の通過を遮る実際の面が存在するしないにかかわらず同じです。